JavaScript Program to Solve Quadratic Equation

This program computes roots of a quadratic equation when its coefficients are known.

The standard form of a quadratic equation is:

ax2 + bx + c = 0, where
a, b and c are real numbers and
a ≠ 0

To find the roots of such equation, we use the formula,

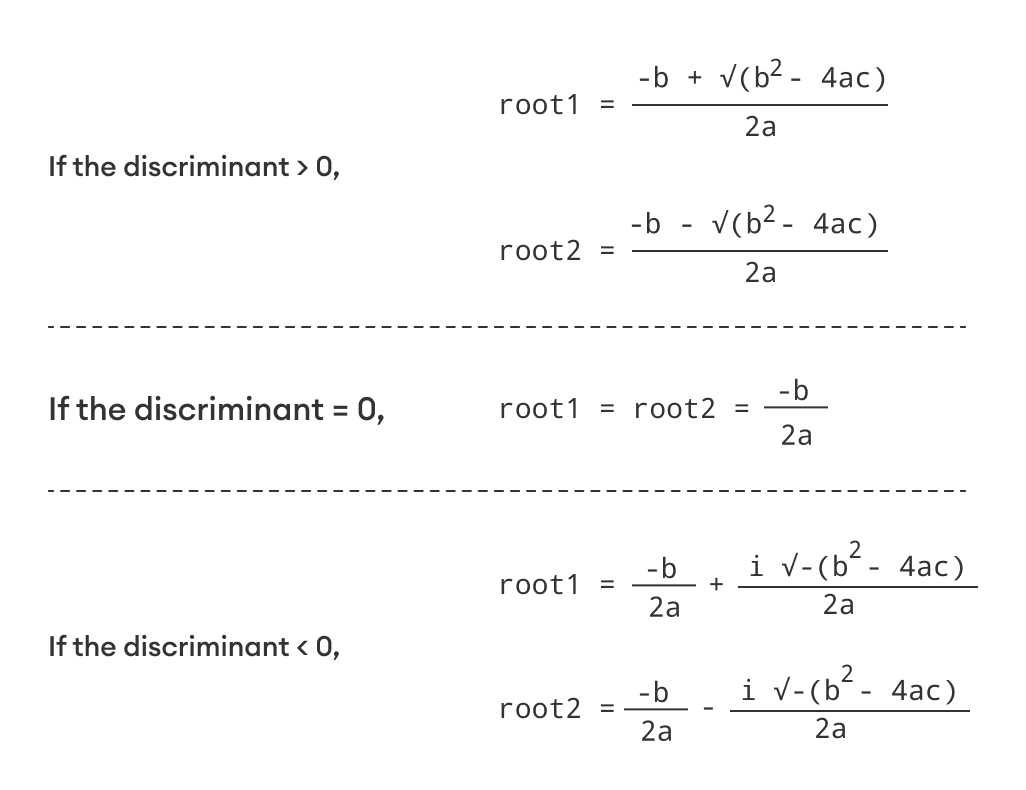
(root1,root2) = (-b ± √b2-4ac)/2

The term b2-4ac is known as the discriminant of a quadratic equation. It tells the nature of the roots.

1. If the discriminant is greater than 0, the roots are real and different.
2. If the discriminant is equal to 0, the roots are real and equal.
3. If the discriminant is less than 0, the roots are complex and different.

Example: Roots of a Quadratic Equation

// program to solve quadratic equation
let root1, root2;

// take input from the user
let a = prompt("Enter the first number: ");
let b = prompt("Enter the second number: ");
let c = prompt("Enter the third number: ");

// calculate discriminant
let discriminant = b * b - 4 * a * c;

// condition for real and different roots
if (discriminant > 0) {
    root1 = (-b + Math.sqrt(discriminant)) / (2 * a);
    root2 = (-b - Math.sqrt(discriminant)) / (2 * a);

    // result
    console.log(`The roots of quadratic equation are ${root1} and ${root2}`);
}

// condition for real and equal roots
else if (discriminant == 0) {
    root1 = root2 = -b / (2 * a);

    // result
    console.log(`The roots of quadratic equation are ${root1} and ${root2}`);
}

// if roots are not real
else {
    let realPart = (-b / (2 * a)).toFixed(2);
    let imagPart = (Math.sqrt(-discriminant) / (2 * a)).toFixed(2);

    // result
    console.log(
    `The roots of quadratic equation are ${realPart} + ${imagPart}i and ${realPart} - ${imagPart}i`
  );
}

Output 1

Enter the first number: 1
Enter the second number: 6
Enter the third number: 5
The roots of quadratic equation are -1 and -5

The above input values satisfy the first if condition. Here, the discriminant will be greater than 0 and the corresponding code is executed.

Output 2

Enter the first number: 1
Enter the second number: -6
Enter the third number: 9
The roots of quadratic equation are 3 and 3

The above input values satisfy the else if condition. Here, the discriminant will be equal to 0 and the corresponding code is executed.

Output 3

Enter the first number: 1
Enter the second number: -3
Enter the third number: 10
The roots of quadratic equation are 1.50 + 2.78i and 1.50 - 2.78i

In the above output, the discriminant will be less than 0 and the corresponding code is executed.

In the above program, the Math.sqrt() method is used to find the square root of a number. You can see that toFixed(2) is also used in the program. This rounds up the decimal number to two decimal values.

The above program uses an if...else statements. If you want to learn more about if...else statements, go to JavaScript if...else Statement.