Go Recursion

In computer programming, a recursive function calls itself. For example,

func recurse() {
  … …
  … …
  recurse()
}

Here, the recurse() function includes the function call within its body. Hence, it is a Go recursive function and this technique is called recursion.

Before you learn about recursion, make sure to know Go Functions.

Example: Recursion in Golang

package main
import "fmt"

func countDown(number int) {

  // display the number
  fmt.Println(number)

  // recursive call by decreasing number
  countDown(number - 1)

  }

func main() {
  countDown(3)
}

Output

Countdown Starts:
3
2
1
0
-1
…
…

In the above example, we have created a function named countDown(). Note that we have added the function call inside the function.

countDown(number - 1)

Here, this is a recursive function call and we are decreasing the value of number in each call.

However, this function will be executed infinitely because we have added the function call directly within the function

To avoid infinite recursion, we use conditional statements and only call the function if the condition is met.

Recursive Function with conditional statement

In this example, we will use an if...else statement to prevent the infinite recursion.

// Program to end the recursive function using if…else

package main
import "fmt"

func countDown(number int) {

  if number > 0 {
    fmt.Println(number)

    // recursive call
    countDown(number - 1)
  } else {
    // ends the recursive function 
    fmt.Println("Countdown Stops")
  }

 }

func main() {
  countDown(3)
}

Output

Countdown Starts
3
Countdown Starts
2
Countdown Starts
1
Countdown Starts
Countdown Stops

In the above example, we have added the recursive call inside the if statement.

if number > 0 {
  fmt.Println(number)

  // recursive call
  countDown(number - 1)
}

Here, we are calling the function only if the number is greater than 0.

If the number is not greater than 0, the recursion ends. This is called the stopping condition.

Working of the program

Example: Go program to calculate the sum of positive numbers

package main
import "fmt"

func sum(number int) int {

  // condition to break recursion
  if number == 0 {
    return 0
  } else {
    return number + sum(number-1)
  }
}

func main() {
  var num = 50

  // function call
  var result = sum(num)

  fmt.Println("Sum:", result)
}

Output

Sum: 1275

In the above example, we have created a recursive function named sum() that calls itself if the value of number is not equal to 0.

return number + sum(number - 1)

In each iteration, we are calling the function by decreasing the value of number by 1.

Here's how the program works:

• In first call, the value of number is 50 which is not equal to 0. So, the else block is executed which returns 50 + sum(49).
• Again, 49 is not equal to 0, so return 49 + sum(48) is executed.
• This process continues until number becomes 0. When number is 0, return 0 is executed and it is added to the other values.
• Hence, finally, 50 + 49 + 48 + ...... + 0 is computed and returned to the main() function.

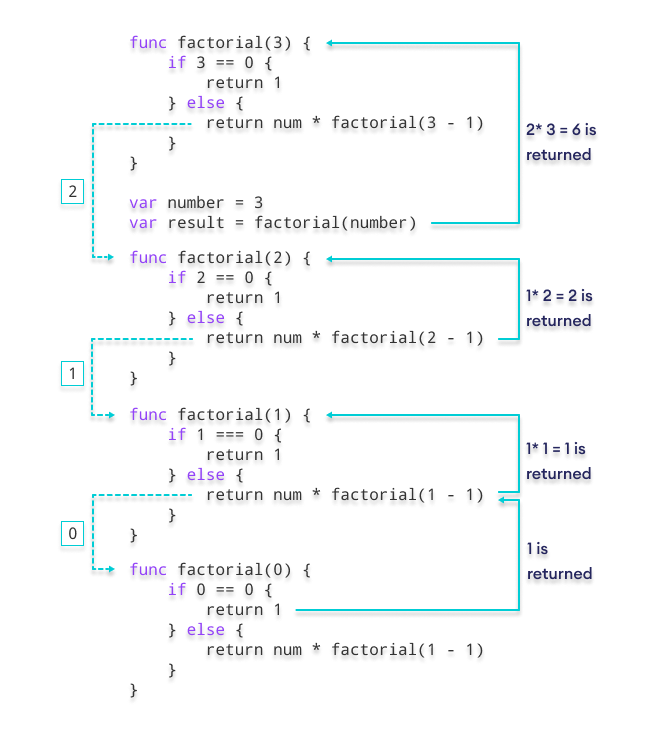
Factorial of a number using Go Recursion

package main
import "fmt"

func factorial (num int) int {

  // condition to break recursion
  if num == 0 {
    return 1
  } else {
    // condition for recursion call
    return num * factorial (num-1)
   }
}

func main() {
  var number = 3
  
  // function call
  var result = factorial (number)

  fmt.Println("The factorial of 3 is", result)
}

Output

The factorial of 3 is 6

In the above example, we have created a recursive function named factorial() that calls itself if the value of num is not equal to 0.

return num * factorial(num - 1)

In each call, we are decreasing the value of num by 1.

Here's how the program works: