A matrix is a two-dimensional data structure where numbers are arranged into rows and columns. For example:
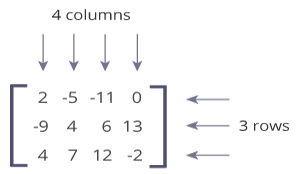
This matrix is a 3x4 (pronounced "three by four") matrix because it has 3 rows and 4 columns.
Python Matrix
Python doesn't have a built-in type for matrices. However, we can treat a list of a list as a matrix. For example:
A = [[1, 4, 5],
[-5, 8, 9]]
We can treat this list of a list as a matrix having 2 rows and 3 columns.

Be sure to learn about Python lists before proceed this article.
Let's see how to work with a nested list.
A = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
print("A =", A)
print("A[1] =", A[1]) # 2nd row
print("A[1][2] =", A[1][2]) # 3rd element of 2nd row
print("A[0][-1] =", A[0][-1]) # Last element of 1st Row
column = []; # empty list
for row in A:
column.append(row[2])
print("3rd column =", column)
When we run the program, the output will be:
A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] A[1] = [-5, 8, 9, 0] A[1][2] = 9 A[0][-1] = 12 3rd column = [5, 9, 11]
Here are few more examples related to Python matrices using nested lists.
Using nested lists as a matrix works for simple computational tasks, however, there is a better way of working with matrices in Python using NumPy package.
NumPy Array
NumPy is a package for scientific computing which has support for a powerful N-dimensional array object. Before you can use NumPy, you need to install it. For more info,
- Visit: How to install NumPy?
- If you are on Windows, download and install anaconda distribution of Python. It comes with NumPy and other several packages related to data science and machine learning.
Once NumPy is installed, you can import and use it.
NumPy provides multidimensional array of numbers (which is actually an object). Let's take an example:
import numpy as np
a = np.array([1, 2, 3])
print(a) # Output: [1, 2, 3]
print(type(a)) # Output: <class 'numpy.ndarray'>
As you can see, NumPy's array class is called ndarray.
How to create a NumPy array?
There are several ways to create NumPy arrays.
1. Array of integers, floats and complex Numbers
import numpy as np
A = np.array([[1, 2, 3], [3, 4, 5]])
print(A)
A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Array of floats
print(A)
A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Array of complex numbers
print(A)
When you run the program, the output will be:
[[1 2 3] [3 4 5]] [[1.1 2. 3. ] [3. 4. 5. ]] [[1.+0.j 2.+0.j 3.+0.j] [3.+0.j 4.+0.j 5.+0.j]]
import numpy as np
zeors_array = np.zeros( (2, 3) )
print(zeors_array)
'''
Output:
[[0. 0. 0.]
[0. 0. 0.]]
'''
ones_array = np.ones( (1, 5), dtype=np.int32 ) // specifying dtype
print(ones_array) # Output: [[1 1 1 1 1]]
Here, we have specified dtype to 32 bits (4 bytes). Hence, this array can take values from -2-31 to 2-31-1.
import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
'''
Output:
A = [0 1 2 3]
B = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
Learn more about other ways of creating a NumPy array.
Matrix Operations
Above, we gave you 3 examples: addition of two matrices, multiplication of two matrices and transpose of a matrix. We used nested lists before to write those programs. Let's see how we can do the same task using NumPy array.
We use + operator to add corresponding elements of two NumPy matrices.
import numpy as np
A = np.array([[2, 4], [5, -6]])
B = np.array([[9, -3], [3, 6]])
C = A + B # element wise addition
print(C)
'''
Output:
[[11 1]
[ 8 0]]
'''
Multiplication of Two Matrices
To multiply two matrices, we use dot() method. Learn more about how numpy.dot works.
Note: * is used for array multiplication (multiplication of corresponding elements of two arrays) not matrix multiplication.
import numpy as np
A = np.array([[3, 6, 7], [5, -3, 0]])
B = np.array([[1, 1], [2, 1], [3, -3]])
C = A.dot(B)
print(C)
'''
Output:
[[ 36 -12]
[ -1 2]]
'''
We use numpy.transpose to compute transpose of a matrix.
import numpy as np
A = np.array([[1, 1], [2, 1], [3, -3]])
print(A.transpose())
'''
Output:
[[ 1 2 3]
[ 1 1 -3]]
'''
As you can see, NumPy made our task much easier.
Access matrix elements, rows and columns
Similar like lists, we can access matrix elements using index. Let's start with a one-dimensional NumPy array.
import numpy as np
A = np.array([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # First element
print("A[2] =", A[2]) # Third element
print("A[-1] =", A[-1]) # Last element
When you run the program, the output will be:
A[0] = 2 A[2] = 6 A[-1] = 10
Now, let's see how we can access elements of a two-dimensional array (which is basically a matrix).
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# First element of first row
print("A[0][0] =", A[0][0])
# Third element of second row
print("A[1][2] =", A[1][2])
# Last element of last row
print("A[-1][-1] =", A[-1][-1])
When we run the program, the output will be:
A[0][0] = 1 A[1][2] = 9 A[-1][-1] = 19
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # First Row
print("A[2] =", A[2]) # Third Row
print("A[-1] =", A[-1]) # Last Row (3rd row in this case)
When we run the program, the output will be:
A[0] = [1, 4, 5, 12] A[2] = [-6, 7, 11, 19] A[-1] = [-6, 7, 11, 19]
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[:,0] =",A[:,0]) # First Column
print("A[:,3] =", A[:,3]) # Fourth Column
print("A[:,-1] =", A[:,-1]) # Last Column (4th column in this case)
When we run the program, the output will be:
A[:,0] = [ 1 -5 -6] A[:,3] = [12 0 19] A[:,-1] = [12 0 19]
If you don't know how this above code works, read slicing of a matrix section of this article.
Slicing of a Matrix
Slicing of a one-dimensional NumPy array is similar to a list. If you don't know how slicing for a list works, visit Understanding Python's slice notation.
Let's take an example:
import numpy as np
letters = np.array([1, 3, 5, 7, 9, 7, 5])
# 3rd to 5th elements
print(letters[2:5]) # Output: [5, 7, 9]
# 1st to 4th elements
print(letters[:-5]) # Output: [1, 3]
# 6th to last elements
print(letters[5:]) # Output:[7, 5]
# 1st to last elements
print(letters[:]) # Output:[1, 3, 5, 7, 9, 7, 5]
# reversing a list
print(letters[::-1]) # Output:[5, 7, 9, 7, 5, 3, 1]
Now, let's see how we can slice a matrix.
import numpy as np
A = np.array([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # two rows, four columns
''' Output:
[[ 1 4 5 12]
[-5 8 9 0]]
'''
print(A[:1,]) # first row, all columns
''' Output:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # all rows, second column
''' Output:
[ 5 9 11]
'''
print(A[:, 2:5]) # all rows, third to the fifth column
'''Output:
[[ 5 12 14]
[ 9 0 17]
[11 19 21]]
'''
As you can see, using NumPy (instead of nested lists) makes it a lot easier to work with matrices, and we haven't even scratched the basics. We suggest you to explore NumPy package in detail especially if you trying to use Python for data science/analytics.
