A function that calls itself is known as a recursive function. And, this technique is known as recursion.
A physical world example would be to place two parallel mirrors facing each other. Any object in between them would be reflected recursively.
Working of Recursion in Swift
func recurse() {
... ...
recurse()
... ...
}
recurse()
Here, the recurse() function is calling itself over and over again. The figure below shows how recursion works.
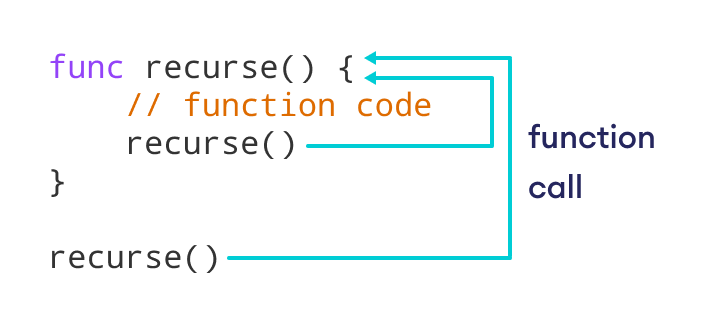
Stopping Condition for Recursion
If we don't mention any condition to break the recursive call, the function will keep calling itself infinitely.
We use the if...else statement (or similar approach) to break the recursion.
Normally, a recursive function has two branches:
- One for recursive calls.
- Another for breaking the call under certain conditions.
For example,
func recurse() {
if(condition) {
// break recursive call
recurse()
}
else {
// recursive call
recurse()
}
}
// function call
recurse()
Example 1: Swift Function Recursion
// program to count down number to 0
func countDown(number: Int) {
// display the number
print(number)
// condition to break recursion
if number == 0 {
print("Countdown Stops")
}
// condition for recursion call
else {
// decrease the number value
countDown(number: number - 1)
}
}
print("Countdown:")
countDown(number:3)
Output
Countdown: 3 2 1 0 Countdown Stops
In the above example, we have created a recursive function named countDown(). Here, the function calls itself until the number passed to it becomes 0.
When the number is equal to 0, the if condition breaks the recursive call.
if number == 0 {
print(Countdown Stops)
}
Working of the program
| Iteration | Function call | number == 0 ? | |
|---|---|---|---|
| 1 | countDown(3) |
3 | false |
| 2 | countDown(2) |
2 | false |
| 3 | countDown(1) |
1 | false |
| 4 | countDown(0) |
0 | true(function call stops) |
Example: Find factorial of a number
func factorial(num: Int) -> Int {
// condition to break recursion
if num == 0 {
return 1
}
// condition for recursive call
else {
return num * factorial(num: num - 1)
}
}
var number = 3
// function call
var result = factorial(num: number)
print("The factorial of 3 is", result)
Output
The factorial of 3 is 6
In the above example, we have a recursive function named factorial(). Notice the statement
return num * factorial(num: num - 1)
Here, we are recursively calling factorial() by decreasing the value of the num parameter.
- Initially, the value of num is 3 inside
factorial(). - In the next recursive call, num becomes 2.
- Similarly, the process continues until num becomes 0.
- When num is equal to 0, the
ifcondition breaks the recursive call.
Working of the Program

Advantages and Disadvantages of Function Recursion
Below are the advantages and disadvantages of using recursion in Swift programming.
1. Advantages
- It makes our code shorter and cleaner.
- Recursion is required in problems concerning data structures and advanced algorithms, such as Graph and Tree Traversal.
2. Disadvantages
- It takes a lot of stack space compared to an iterative program.
- It uses more processor time.
- It can be more difficult to debug compared to an equivalent iterative program.