Bubble sort is a sorting algorithm that compares two adjacent elements and swaps them until they are in the intended order.
Just like the movement of air bubbles in the water that rise up to the surface, each element of the array move to the end in each iteration. Therefore, it is called a bubble sort.
Working of Bubble Sort
Suppose we are trying to sort the elements in ascending order.
1. First Iteration (Compare and Swap)
- Starting from the first index, compare the first and the second elements.
- If the first element is greater than the second element, they are swapped.
- Now, compare the second and the third elements. Swap them if they are not in order.
- The above process goes on until the last element.
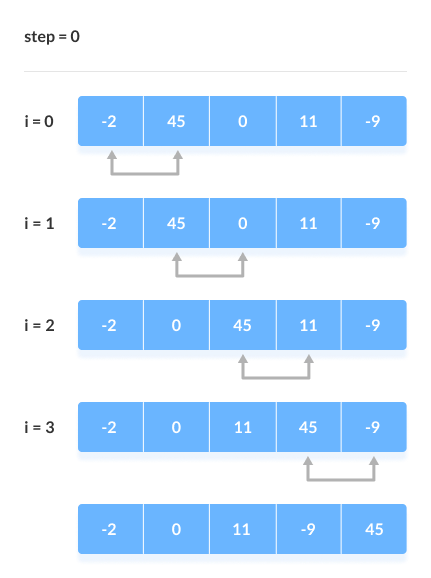
Compare the Adjacent Elements
2. Remaining Iteration
The same process goes on for the remaining iterations.
After each iteration, the largest element among the unsorted elements is placed at the end.
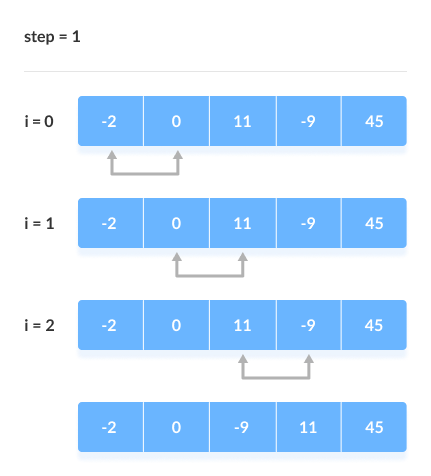
In each iteration, the comparison takes place up to the last unsorted element.
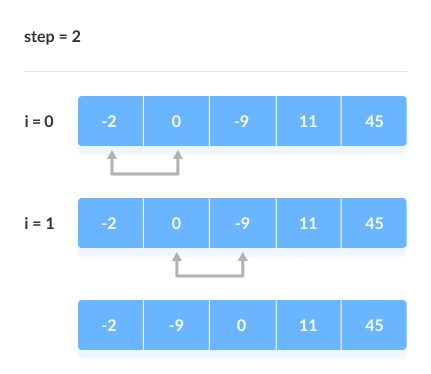
The array is sorted when all the unsorted elements are placed at their correct positions.
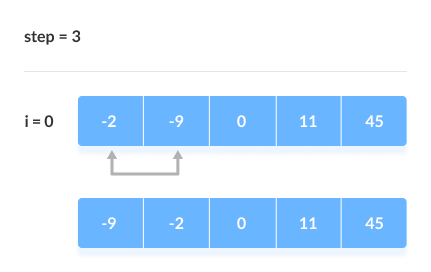
Bubble Sort Algorithm
bubbleSort(array)
for i <- 1 to indexOfLastUnsortedElement-1
if leftElement > rightElement
swap leftElement and rightElement
end bubbleSort
Bubble Sort Code in Python, Java and C/C++
# Bubble sort in Python
def bubbleSort(array):
# loop to access each array element
for i in range(len(array)):
# loop to compare array elements
for j in range(0, len(array) - i - 1):
# compare two adjacent elements
# change > to < to sort in descending order
if array[j] > array[j + 1]:
# swapping elements if elements
# are not in the intended order
temp = array[j]
array[j] = array[j+1]
array[j+1] = temp
data = [-2, 45, 0, 11, -9]
bubbleSort(data)
print('Sorted Array in Ascending Order:')
print(data)
// Bubble sort in Java
import java.util.Arrays;
class Main {
// perform the bubble sort
static void bubbleSort(int array[]) {
int size = array.length;
// loop to access each array element
for (int i = 0; i < size - 1; i++)
// loop to compare array elements
for (int j = 0; j < size - i - 1; j++)
// compare two adjacent elements
// change > to < to sort in descending order
if (array[j] > array[j + 1]) {
// swapping occurs if elements
// are not in the intended order
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
public static void main(String args[]) {
int[] data = { -2, 45, 0, 11, -9 };
// call method using class name
Main.bubbleSort(data);
System.out.println("Sorted Array in Ascending Order:");
System.out.println(Arrays.toString(data));
}
}
// Bubble sort in C
#include <stdio.h>
// perform the bubble sort
void bubbleSort(int array[], int size) {
// loop to access each array element
for (int step = 0; step < size - 1; ++step) {
// loop to compare array elements
for (int i = 0; i < size - step - 1; ++i) {
// compare two adjacent elements
// change > to < to sort in descending order
if (array[i] > array[i + 1]) {
// swapping occurs if elements
// are not in the intended order
int temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
}
}
}
}
// print array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
printf("%d ", array[i]);
}
printf("\n");
}
int main() {
int data[] = {-2, 45, 0, 11, -9};
// find the array's length
int size = sizeof(data) / sizeof(data[0]);
bubbleSort(data, size);
printf("Sorted Array in Ascending Order:\n");
printArray(data, size);
}
// Bubble sort in C++
#include <iostream>
using namespace std;
// perform bubble sort
void bubbleSort(int array[], int size) {
// loop to access each array element
for (int step = 0; step < size; ++step) {
// loop to compare array elements
for (int i = 0; i < size - step; ++i) {
// compare two adjacent elements
// change > to < to sort in descending order
if (array[i] > array[i + 1]) {
// swapping elements if elements
// are not in the intended order
int temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
}
}
}
}
// print array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
cout << " " << array[i];
}
cout << "\n";
}
int main() {
int data[] = {-2, 45, 0, 11, -9};
// find array's length
int size = sizeof(data) / sizeof(data[0]);
bubbleSort(data, size);
cout << "Sorted Array in Ascending Order:\n";
printArray(data, size);
}
Optimized Bubble Sort Algorithm
In the above algorithm, all the comparisons are made even if the array is already sorted.
This increases the execution time.
To solve this, we can introduce an extra variable swapped. The value of swapped is set true if there occurs swapping of elements. Otherwise, it is set false.
After an iteration, if there is no swapping, the value of swapped will be false. This means elements are already sorted and there is no need to perform further iterations.
This will reduce the execution time and helps to optimize the bubble sort.
Algorithm for optimized bubble sort is
bubbleSort(array)
swapped <- false
for i <- 1 to indexOfLastUnsortedElement-1
if leftElement > rightElement
swap leftElement and rightElement
swapped <- true
end bubbleSort
Optimized Bubble Sort in Python, Java, and C/C++
# Optimized Bubble sort in Python
def bubbleSort(array):
# loop through each element of array
for i in range(len(array)):
# keep track of swapping
swapped = False
# loop to compare array elements
for j in range(0, len(array) - i - 1):
# compare two adjacent elements
# change > to < to sort in descending order
if array[j] > array[j + 1]:
# swapping occurs if elements
# are not in the intended order
temp = array[j]
array[j] = array[j+1]
array[j+1] = temp
swapped = True
# no swapping means the array is already sorted
# so no need for further comparison
if not swapped:
break
data = [-2, 45, 0, 11, -9]
bubbleSort(data)
print('Sorted Array in Ascending Order:')
print(data)
// Optimized Bubble sort in Java
import java.util.Arrays;
class Main {
// perform the bubble sort
static void bubbleSort(int array[]) {
int size = array.length;
// loop to access each array element
for (int i = 0; i < (size-1); i++) {
// check if swapping occurs
boolean swapped = false;
// loop to compare adjacent elements
for (int j = 0; j < (size-i-1); j++) {
// compare two array elements
// change > to < to sort in descending order
if (array[j] > array[j + 1]) {
// swapping occurs if elements
// are not in the intended order
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
swapped = true;
}
}
// no swapping means the array is already sorted
// so no need for further comparison
if (!swapped)
break;
}
}
public static void main(String args[]) {
int[] data = { -2, 45, 0, 11, -9 };
// call method using the class name
Main.bubbleSort(data);
System.out.println("Sorted Array in Ascending Order:");
System.out.println(Arrays.toString(data));
}
}
// Optimized Bubble sort in C
#include
// perform the bubble sort
void bubbleSort(int array[], int size) {
// loop to access each array element
for (int step = 0; step < size - 1; ++step) {
// check if swapping occurs
int swapped = 0;
// loop to compare array elements
for (int i = 0; i < size - step - 1; ++i) {
// compare two array elements
// change > to < to sort in descending order
if (array[i] > array[i + 1]) {
// swapping occurs if elements
// are not in the intended order
int temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
swapped = 1;
}
}
// no swapping means the array is already sorted
// so no need for further comparison
if (swapped == 0) {
break;
}
}
}
// print array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
printf("%d ", array[i]);
}
printf("\n");
}
// main method
int main() {
int data[] = {-2, 45, 0, 11, -9};
// find the array's length
int size = sizeof(data) / sizeof(data[0]);
bubbleSort(data, size);
printf("Sorted Array in Ascending Order:\n");
printArray(data, size);
}
// Optimized bubble sort in C++
#include
using namespace std;
// perform bubble sort
void bubbleSort(int array[], int size) {
// loop to access each array element
for (int step = 0; step < (size-1); ++step) {
// check if swapping occurs
int swapped = 0;
// loop to compare two elements
for (int i = 0; i < (size-step-1); ++i) {
// compare two array elements
// change > to < to sort in descending order
if (array[i] > array[i + 1]) {
// swapping occurs if elements
// are not in intended order
int temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
swapped = 1;
}
}
// no swapping means the array is already sorted
// so no need of further comparison
if (swapped == 0)
break;
}
}
// print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
cout << " " << array[i];
}
cout << "\n";
}
int main() {
int data[] = {-2, 45, 0, 11, -9};
// find the array's length
int size = sizeof(data) / sizeof(data[0]);
bubbleSort(data, size);
cout << "Sorted Array in Ascending Order:\n";
printArray(data, size);
}
Bubble Sort Complexity
| Time Complexity | |
|---|---|
| Best | O(n) |
| Worst | O(n2) |
| Average | O(n2) |
| Space Complexity | O(1) |
| Stability | Yes |
Complexity in Detail
Bubble Sort compares the adjacent elements.
| Cycle | Number of Comparisons |
|---|---|
| 1st | (n-1) |
| 2nd | (n-2) |
| 3rd | (n-3) |
| ....... | ...... |
| last | 1 |
Hence, the number of comparisons is
(n-1) + (n-2) + (n-3) +.....+ 1 = n(n-1)/2
nearly equals to n2
Hence, Complexity: O(n2)
Also, if we observe the code, bubble sort requires two loops. Hence, the complexity is n*n = n2
1. Time Complexities
- Worst Case Complexity:
O(n2)
If we want to sort in ascending order and the array is in descending order then the worst case occurs. - Best Case Complexity:
O(n)
If the array is already sorted, then there is no need for sorting. - Average Case Complexity:
O(n2)
It occurs when the elements of the array are in jumbled order (neither ascending nor descending).
2. Space Complexity
- Space complexity is
O(1)because an extra variable is used for swapping. - In the optimized bubble sort algorithm, two extra variables are used. Hence, the space complexity will be
O(2).
Bubble Sort Applications
Bubble sort is used if
- complexity does not matter
- short and simple code is preferred