Counting sort is a sorting algorithm that sorts the elements of an array by counting the number of occurrences of each unique element in the array. The count is stored in an auxiliary array and the sorting is done by mapping the count as an index of the auxiliary array.
Working of Counting Sort
- Find out the maximum element (let it be
max) from the given array.
Given array - Initialize an array of length
max+1with all elements 0. This array is used for storing the count of the elements in the array.
Count array - Store the count of each element at their respective index in
countarray.
For example: if the count of element 3 is 2 then, 2 is stored in the 3rd position of count array. If element "5" is not present in the array, then 0 is stored in 5th position.
Count of each element stored - Store cumulative sum of the elements of the count array. It helps in placing the elements into the correct index of the sorted array.

Cumulative count - Find the index of each element of the original array in the count array. This gives the cumulative count. Place the element at the index calculated as shown in figure below.
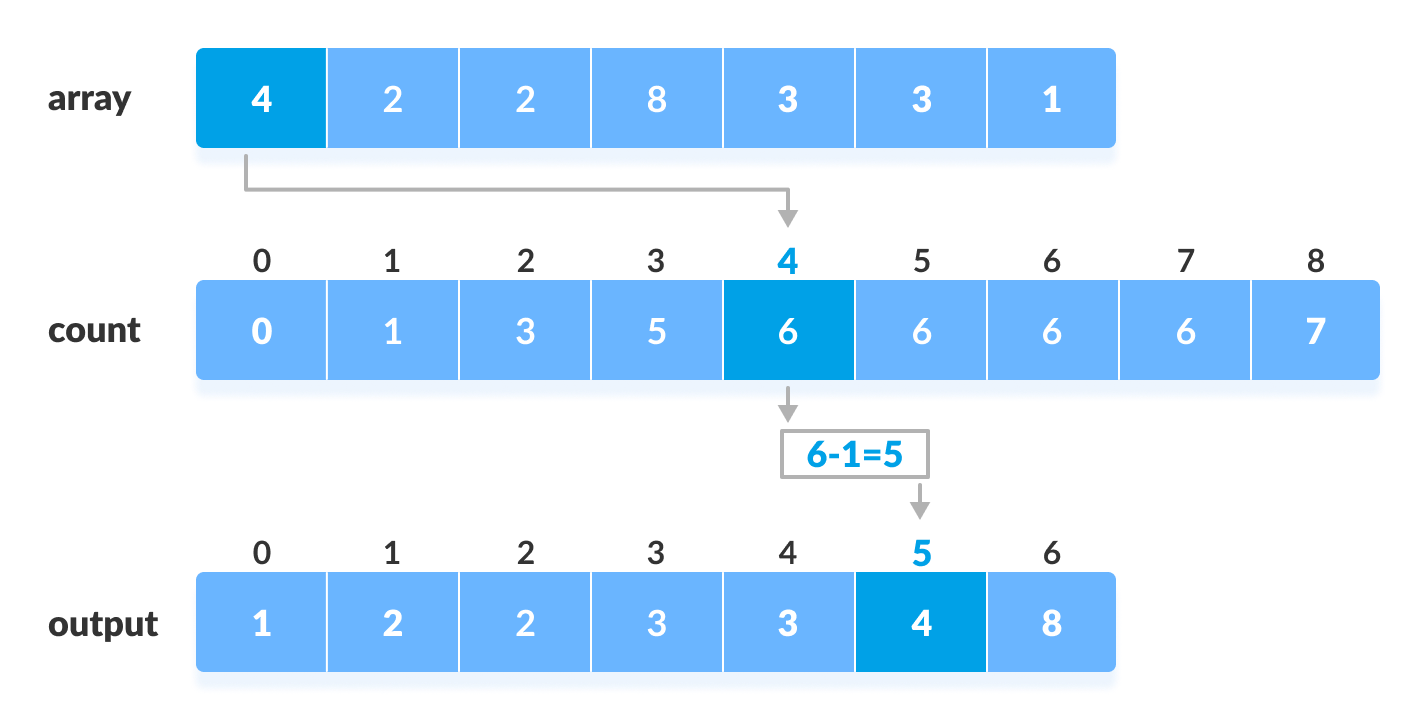
Counting sort - After placing each element at its correct position, decrease its count by one.
Counting Sort Algorithm
countingSort(array, size)
max <- find largest element in array
initialize count array with all zeros
for j <- 0 to size
find the total count of each unique element and
store the count at jth index in count array
for i <- 1 to max
find the cumulative sum and store it in count array itself
for j <- size down to 1
restore the elements to array
decrease count of each element restored by 1
Counting Sort Code in Python, Java, and C/C++
# Counting sort in Python programming
def countingSort(array):
size = len(array)
output = [0] * size
# Initialize count array
count = [0] * (max(array) + 1)
# Store the count of each elements in count array
for i in range(0, size):
count[array[i]] += 1
# Store the cummulative count
for i in range(1, (max(array) + 1)):
count[i] += count[i - 1]
# Find the index of each element of the original array in count array
# place the elements in output array
i = size - 1
while i >= 0:
output[count[array[i]] - 1] = array[i]
count[array[i]] -= 1
i -= 1
# Copy the sorted elements into original array
for i in range(0, size):
array[i] = output[i]
data = [4, 2, 2, 8, 3, 3, 1]
countingSort(data)
print("Sorted Array in Ascending Order: ")
print(data)
// Counting sort in Java programming
import java.util.Arrays;
class CountingSort {
void countSort(int array[], int size) {
int[] output = new int[size + 1];
// Find the largest element of the array
int max = array[0];
for (int i = 1; i < size; i++) {
if (array[i] > max)
max = array[i];
}
int[] count = new int[max + 1];
// Initialize count array with all zeros.
for (int i = 0; i < max; ++i) {
count[i] = 0;
}
// Store the count of each element
for (int i = 0; i < size; i++) {
count[array[i]]++;
}
// Store the cummulative count of each array
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
// Find the index of each element of the original array in count array, and
// place the elements in output array
for (int i = size - 1; i >= 0; i--) {
output[count[array[i]] - 1] = array[i];
count[array[i]]--;
}
// Copy the sorted elements into original array
for (int i = 0; i < size; i++) {
array[i] = output[i];
}
}
// Driver code
public static void main(String args[]) {
int[] data = { 4, 2, 2, 8, 3, 3, 1 };
int size = data.length;
CountingSort cs = new CountingSort();
cs.countSort(data, size);
System.out.println("Sorted Array in Ascending Order: ");
System.out.println(Arrays.toString(data));
}
}
// Counting sort in C programming
#include <stdio.h>
void countingSort(int array[], int size) {
int output[10];
// Find the largest element of the array
int max = array[0];
for (int i = 1; i < size; i++) {
if (array[i] > max)
max = array[i];
}
// The size of count must be at least (max+1) but
// we cannot declare it as int count(max+1) in C as
// it does not support dynamic memory allocation.
// So, its size is provided statically.
int count[10];
// Initialize count array with all zeros.
for (int i = 0; i <= max; ++i) {
count[i] = 0;
}
// Store the count of each element
for (int i = 0; i < size; i++) {
count[array[i]]++;
}
// Store the cummulative count of each array
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
// Find the index of each element of the original array in count array, and
// place the elements in output array
for (int i = size - 1; i >= 0; i--) {
output[count[array[i]] - 1] = array[i];
count[array[i]]--;
}
// Copy the sorted elements into original array
for (int i = 0; i < size; i++) {
array[i] = output[i];
}
}
// Function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
printf("%d ", array[i]);
}
printf("\n");
}
// Driver code
int main() {
int array[] = {4, 2, 2, 8, 3, 3, 1};
int n = sizeof(array) / sizeof(array[0]);
countingSort(array, n);
printArray(array, n);
}
// Counting sort in C++ programming
#include <iostream>
using namespace std;
void countSort(int array[], int size) {
// The size of count must be at least the (max+1) but
// we cannot assign declare it as int count(max+1) in C++ as
// it does not support dynamic memory allocation.
// So, its size is provided statically.
int output[10];
int count[10];
int max = array[0];
// Find the largest element of the array
for (int i = 1; i < size; i++) {
if (array[i] > max)
max = array[i];
}
// Initialize count array with all zeros.
for (int i = 0; i <= max; ++i) {
count[i] = 0;
}
// Store the count of each element
for (int i = 0; i < size; i++) {
count[array[i]]++;
}
// Store the cummulative count of each array
for (int i = 1; i <= max; i++) {
count[i] += count[i - 1];
}
// Find the index of each element of the original array in count array, and
// place the elements in output array
for (int i = size - 1; i >= 0; i--) {
output[count[array[i]] - 1] = array[i];
count[array[i]]--;
}
// Copy the sorted elements into original array
for (int i = 0; i < size; i++) {
array[i] = output[i];
}
}
// Function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; i++)
cout << array[i] << " ";
cout << endl;
}
// Driver code
int main() {
int array[] = {4, 2, 2, 8, 3, 3, 1};
int n = sizeof(array) / sizeof(array[0]);
countSort(array, n);
printArray(array, n);
}
Complexity
| Time Complexity | |
|---|---|
| Best | O(n+max) |
| Worst | O(n+max) |
| Average | O(n+max) |
| Space Complexity | O(max) |
| Stability | Yes |
Time Complexities
There are mainly four main loops. (Finding the greatest value can be done outside the function.)
| for-loop | time of counting |
|---|---|
| 1st | O(max) |
| 2nd | O(size) |
| 3rd | O(max) |
| 4th | O(size) |
Overall complexity = O(max)+O(size)+O(max)+O(size) = O(max+size)
- Worst Case Complexity:
O(n+max) - Best Case Complexity:
O(n+max) - Average Case Complexity:
O(n+max)
In all the above cases, the complexity is the same because no matter how the elements are placed in the array, the algorithm goes through n+max times.
There is no comparison between any elements, so it is better than comparison based sorting techniques. But, it is bad if the integers are very large because the array of that size should be made.
Space Complexity
The space complexity of Counting Sort is O(max). Larger the range of elements, larger is the space complexity.
Counting Sort Applications
Counting sort is used when:
- there are smaller integers with multiple counts.
- linear complexity is the need.
