Deque or Double Ended Queue is a type of queue in which insertion and removal of elements can either be performed from the front or the rear. Thus, it does not follow FIFO rule (First In First Out).

Types of Deque
- Input Restricted Deque
In this deque, input is restricted at a single end but allows deletion at both the ends. - Output Restricted Deque
In this deque, output is restricted at a single end but allows insertion at both the ends.
Operations on a Deque
Below is the circular array implementation of deque. In a circular array, if the array is full, we start from the beginning.
But in a linear array implementation, if the array is full, no more elements can be inserted. In each of the operations below, if the array is full, "overflow message" is thrown.
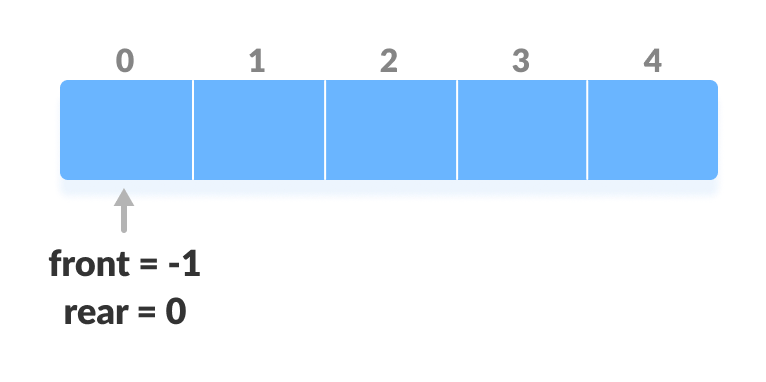
Before performing the following operations, these steps are followed.
- Take an array (deque) of size n.
- Set two pointers
front = -1andrear = 0.
1. Insert at the Front
This operation adds an element at the front.
- Check if the deque is full.

Check the position of front - If the deque is full (i.e.
(front == 0 && rear == n - 1) || (front == rear + 1)), insertion operation cannot be performed (overflow condition). - If the deque is empty, reinitialize
front = 0. And, add the new key intoarray[front]. - If
front = 0, reinitializefront = n-1(last index).
Shift front to the end - Else, decrease front by 1.
- Add the new key 5 into
array[front].
Insert the element at Front
2. Insert at the Rear
This operation adds an element to the rear.
- Check if the deque is full.

Check if deque is full - If the deque is full, insertion operation cannot be performed (overflow condition).
- If the deque is empty, reinitialize
rear = 0. And, add the new key intoarray[rear]. - If
rear = n - 1, reinitializereal = 0(first index). - Else, increase rear by 1.

Increase the rear - Add the new key 5 into
array[rear].
Insert the element at rear
3. Delete from the Front
The operation deletes an element from the front.
- Check if the deque is empty.

Check if deque is empty - If the deque is empty (i.e.
front = -1), deletion cannot be performed (underflow condition). - If the deque has only one element (i.e.
front = rear), setfront = -1andrear = -1. - Else if front is at the last index (i.e.
front = n - 1), setfront = 0. - Else,
front = front + 1.
Increase the front
4. Delete from the Rear
This operation deletes an element from the rear.
- Check if the deque is empty.

Check if deque is empty - If the deque is empty (i.e.
front = -1), deletion cannot be performed (underflow condition). - If the deque has only one element (i.e.
front = rear), setfront = -1andrear = -1, else follow the steps below. - If rear is at the first index (i.e.
rear = 0), reinitializerear = n - 1. - Else,
rear = rear - 1.
Decrease the rear
5. Check Empty
This operation checks if the deque is empty. If front = -1, the deque is empty.
6. Check Full
This operation checks if the deque is full. If front = 0 and rear = n - 1 OR front = rear + 1, the deque is full.
Deque Implementation in Python, Java, C, and C++
# Deque implementaion in python
class Deque:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def addRear(self, item):
self.items.append(item)
def addFront(self, item):
self.items.insert(0, item)
def removeFront(self):
return self.items.pop(0)
def removeRear(self):
return self.items.pop()
def size(self):
return len(self.items)
d = Deque()
print(d.isEmpty())
d.addRear(8)
d.addRear(5)
d.addFront(7)
d.addFront(10)
print(d.size())
print(d.isEmpty())
d.addRear(11)
print(d.removeRear())
print(d.removeFront())
d.addFront(55)
d.addRear(45)
print(d.items)
// Deque implementation in Java
class Deque {
static final int MAX = 100;
int arr[];
int front;
int rear;
int size;
public Deque(int size) {
arr = new int[MAX];
front = -1;
rear = 0;
this.size = size;
}
boolean isFull() {
return ((front == 0 && rear == size - 1) || front == rear + 1);
}
boolean isEmpty() {
return (front == -1);
}
void insertfront(int key) {
if (isFull()) {
System.out.println("Overflow");
return;
}
if (front == -1) {
front = 0;
rear = 0;
}
else if (front == 0)
front = size - 1;
else
front = front - 1;
arr[front] = key;
}
void insertrear(int key) {
if (isFull()) {
System.out.println(" Overflow ");
return;
}
if (front == -1) {
front = 0;
rear = 0;
}
else if (rear == size - 1)
rear = 0;
else
rear = rear + 1;
arr[rear] = key;
}
void deletefront() {
if (isEmpty()) {
System.out.println("Queue Underflow\n");
return;
}
// Deque has only one element
if (front == rear) {
front = -1;
rear = -1;
} else if (front == size - 1)
front = 0;
else
front = front + 1;
}
void deleterear() {
if (isEmpty()) {
System.out.println(" Underflow");
return;
}
if (front == rear) {
front = -1;
rear = -1;
} else if (rear == 0)
rear = size - 1;
else
rear = rear - 1;
}
int getFront() {
if (isEmpty()) {
System.out.println(" Underflow");
return -1;
}
return arr[front];
}
int getRear() {
if (isEmpty() || rear < 0) {
System.out.println(" Underflow\n");
return -1;
}
return arr[rear];
}
public static void main(String[] args) {
Deque dq = new Deque(4);
System.out.println("Insert element at rear end : 12 ");
dq.insertrear(12);
System.out.println("insert element at rear end : 14 ");
dq.insertrear(14);
System.out.println("get rear element : " + dq.getRear());
dq.deleterear();
System.out.println("After delete rear element new rear become : " + dq.getRear());
System.out.println("inserting element at front end");
dq.insertfront(13);
System.out.println("get front element: " + dq.getFront());
dq.deletefront();
System.out.println("After delete front element new front become : " + +dq.getFront());
}
}
// Deque implementation in C
#include <stdio.h>
#define MAX 10
void addFront(int *, int, int *, int *);
void addRear(int *, int, int *, int *);
int delFront(int *, int *, int *);
int delRear(int *, int *, int *);
void display(int *);
int count(int *);
int main() {
int arr[MAX];
int front, rear, i, n;
front = rear = -1;
for (i = 0; i < MAX; i++)
arr[i] = 0;
addRear(arr, 5, &front, &rear);
addFront(arr, 12, &front, &rear);
addRear(arr, 11, &front, &rear);
addFront(arr, 5, &front, &rear);
addRear(arr, 6, &front, &rear);
addFront(arr, 8, &front, &rear);
printf("\nElements in a deque: ");
display(arr);
i = delFront(arr, &front, &rear);
printf("\nremoved item: %d", i);
printf("\nElements in a deque after deletion: ");
display(arr);
addRear(arr, 16, &front, &rear);
addRear(arr, 7, &front, &rear);
printf("\nElements in a deque after addition: ");
display(arr);
i = delRear(arr, &front, &rear);
printf("\nremoved item: %d", i);
printf("\nElements in a deque after deletion: ");
display(arr);
n = count(arr);
printf("\nTotal number of elements in deque: %d", n);
}
void addFront(int *arr, int item, int *pfront, int *prear) {
int i, k, c;
if (*pfront == 0 && *prear == MAX - 1) {
printf("\nDeque is full.\n");
return;
}
if (*pfront == -1) {
*pfront = *prear = 0;
arr[*pfront] = item;
return;
}
if (*prear != MAX - 1) {
c = count(arr);
k = *prear + 1;
for (i = 1; i <= c; i++) {
arr[k] = arr[k - 1];
k--;
}
arr[k] = item;
*pfront = k;
(*prear)++;
} else {
(*pfront)--;
arr[*pfront] = item;
}
}
void addRear(int *arr, int item, int *pfront, int *prear) {
int i, k;
if (*pfront == 0 && *prear == MAX - 1) {
printf("\nDeque is full.\n");
return;
}
if (*pfront == -1) {
*prear = *pfront = 0;
arr[*prear] = item;
return;
}
if (*prear == MAX - 1) {
k = *pfront - 1;
for (i = *pfront - 1; i < *prear; i++) {
k = i;
if (k == MAX - 1)
arr[k] = 0;
else
arr[k] = arr[i + 1];
}
(*prear)--;
(*pfront)--;
}
(*prear)++;
arr[*prear] = item;
}
int delFront(int *arr, int *pfront, int *prear) {
int item;
if (*pfront == -1) {
printf("\nDeque is empty.\n");
return 0;
}
item = arr[*pfront];
arr[*pfront] = 0;
if (*pfront == *prear)
*pfront = *prear = -1;
else
(*pfront)++;
return item;
}
int delRear(int *arr, int *pfront, int *prear) {
int item;
if (*pfront == -1) {
printf("\nDeque is empty.\n");
return 0;
}
item = arr[*prear];
arr[*prear] = 0;
(*prear)--;
if (*prear == -1)
*pfront = -1;
return item;
}
void display(int *arr) {
int i;
printf("\n front: ");
for (i = 0; i < MAX; i++)
printf(" %d", arr[i]);
printf(" :rear");
}
int count(int *arr) {
int c = 0, i;
for (i = 0; i < MAX; i++) {
if (arr[i] != 0)
c++;
}
return c;
}
// Deque implementation in C++
#include <iostream>
using namespace std;
#define MAX 10
class Deque {
int arr[MAX];
int front;
int rear;
int size;
public:
Deque(int size) {
front = -1;
rear = 0;
this->size = size;
}
void insertfront(int key);
void insertrear(int key);
void deletefront();
void deleterear();
bool isFull();
bool isEmpty();
int getFront();
int getRear();
};
bool Deque::isFull() {
return ((front == 0 && rear == size - 1) ||
front == rear + 1);
}
bool Deque::isEmpty() {
return (front == -1);
}
void Deque::insertfront(int key) {
if (isFull()) {
cout << "Overflow\n"
<< endl;
return;
}
if (front == -1) {
front = 0;
rear = 0;
}
else if (front == 0)
front = size - 1;
else
front = front - 1;
arr[front] = key;
}
void Deque ::insertrear(int key) {
if (isFull()) {
cout << " Overflow\n " << endl;
return;
}
if (front == -1) {
front = 0;
rear = 0;
}
else if (rear == size - 1)
rear = 0;
else
rear = rear + 1;
arr[rear] = key;
}
void Deque ::deletefront() {
if (isEmpty()) {
cout << "Queue Underflow\n"
<< endl;
return;
}
if (front == rear) {
front = -1;
rear = -1;
} else if (front == size - 1)
front = 0;
else
front = front + 1;
}
void Deque::deleterear() {
if (isEmpty()) {
cout << " Underflow\n"
<< endl;
return;
}
if (front == rear) {
front = -1;
rear = -1;
} else if (rear == 0)
rear = size - 1;
else
rear = rear - 1;
}
int Deque::getFront() {
if (isEmpty()) {
cout << " Underflow\n"
<< endl;
return -1;
}
return arr[front];
}
int Deque::getRear() {
if (isEmpty() || rear < 0) {
cout << " Underflow\n"
<< endl;
return -1;
}
return arr[rear];
}
int main() {
Deque dq(4);
cout << "insert element at rear end \n";
dq.insertrear(5);
dq.insertrear(11);
cout << "rear element: "
<< dq.getRear() << endl;
dq.deleterear();
cout << "after deletion of the rear element, the new rear element: " << dq.getRear() << endl;
cout << "insert element at front end \n";
dq.insertfront(8);
cout << "front element: " << dq.getFront() << endl;
dq.deletefront();
cout << "after deletion of front element new front element: " << dq.getFront() << endl;
}
Time Complexity
The time complexity of all the above operations is constant i.e. O(1).










