Floyd-Warshall Algorithm is an algorithm for finding the shortest path between all the pairs of vertices in a weighted graph. This algorithm works for both the directed and undirected weighted graphs. But, it does not work for the graphs with negative cycles (where the sum of the edges in a cycle is negative).
A weighted graph is a graph in which each edge has a numerical value associated with it.
Floyd-Warhshall algorithm is also called as Floyd's algorithm, Roy-Floyd algorithm, Roy-Warshall algorithm, or WFI algorithm.
This algorithm follows the dynamic programming approach to find the shortest paths.
How Floyd-Warshall Algorithm Works?
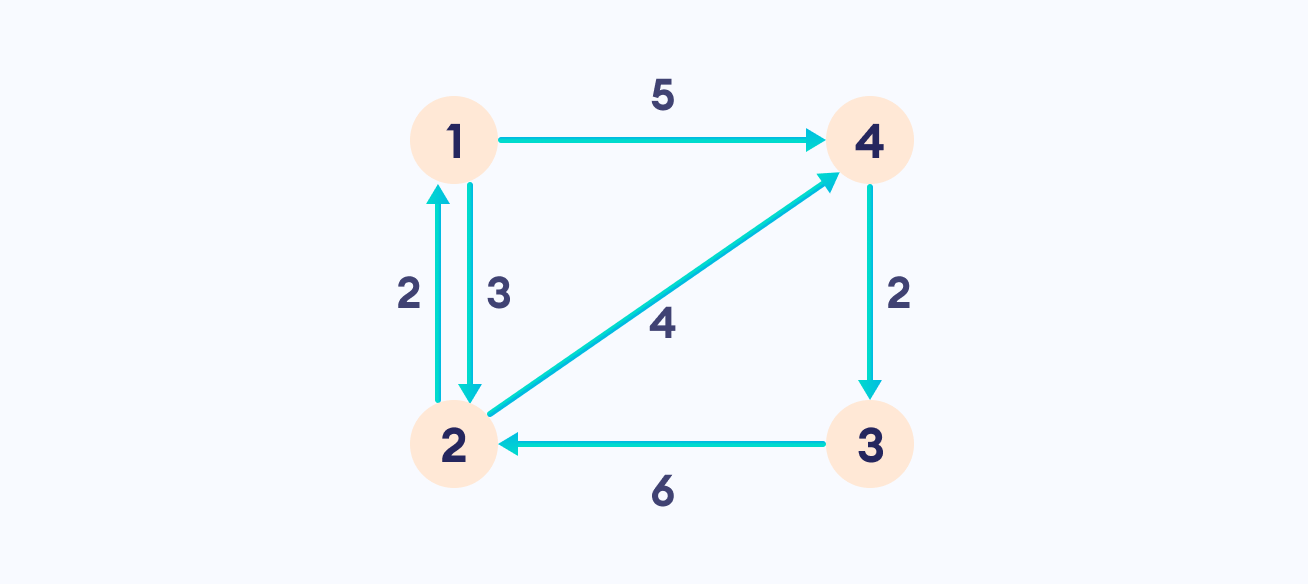
Let the given graph be:

Follow the steps below to find the shortest path between all the pairs of vertices.
- Create a matrix
A0of dimensionn*nwhere n is the number of vertices. The row and the column are indexed as i and j respectively. i and j are the vertices of the graph.
Each cell A[i][j] is filled with the distance from theithvertex to thejthvertex. If there is no path fromithvertex tojthvertex, the cell is left as infinity.
Fill each cell with the distance between ith and jth vertex - Now, create a matrix
A1using matrixA0. The elements in the first column and the first row are left as they are. The remaining cells are filled in the following way.
Let k be the intermediate vertex in the shortest path from source to destination. In this step, k is the first vertex.A[i][j]is filled with(A[i][k] + A[k][j]) if (A[i][j] > A[i][k] + A[k][j]).
That is, if the direct distance from the source to the destination is greater than the path through the vertex k, then the cell is filled withA[i][k] + A[k][j].
In this step, k is vertex 1. We calculate the distance from source vertex to destination vertex through this vertex k.
Calculate the distance from the source vertex to destination vertex through this vertex k
For example: ForA1[2, 4], the direct distance from vertex 2 to 4 is 4 and the sum of the distance from vertex 2 to 4 through vertex (ie. from vertex 2 to 1 and from vertex 1 to 4) is 7. Since4 < 7,A0[2, 4]is filled with 4. - Similarly,
A2is created usingA1. The elements in the second column and the second row are left as they are.
In this step, k is the second vertex (i.e. vertex 2). The remaining steps are the same as in step 2.
Calculate the distance from the source vertex to destination vertex through this vertex 2 - Similarly,
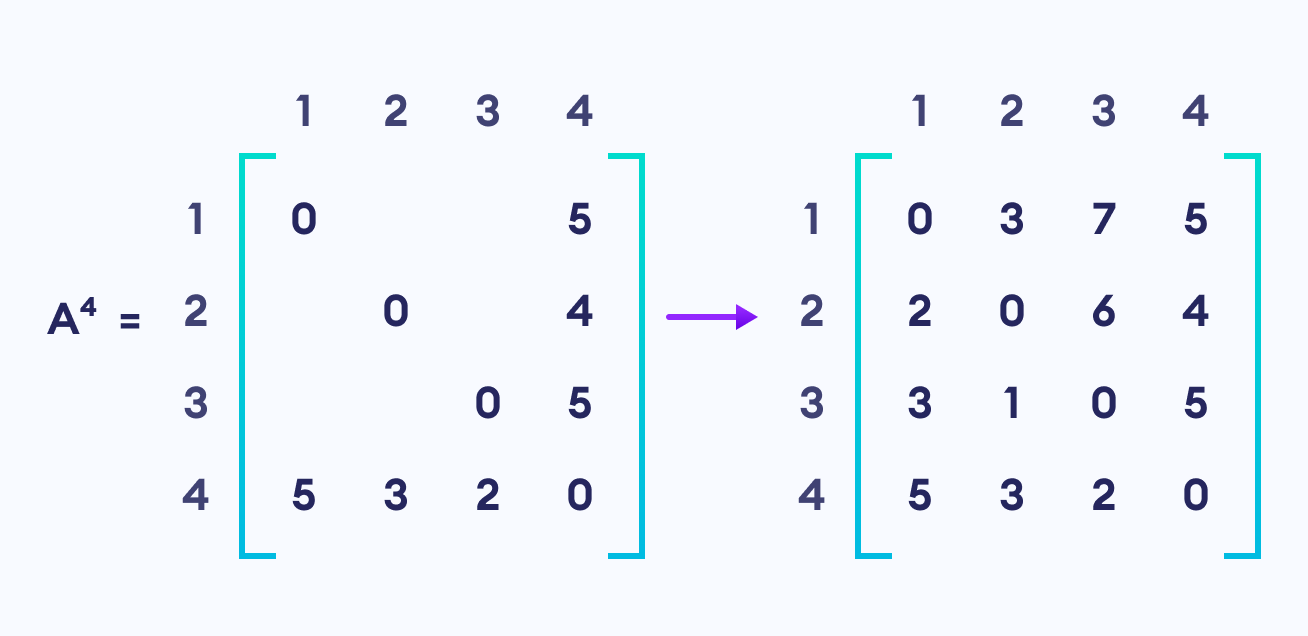
A3andA4is also created.
Calculate the distance from the source vertex to destination vertex through this vertex 3 
Calculate the distance from the source vertex to destination vertex through this vertex 4 A4gives the shortest path between each pair of vertices.
Floyd-Warshall Algorithm
n = no of vertices
A = matrix of dimension n*n
for k = 1 to n
for i = 1 to n
for j = 1 to n
Ak[i, j] = min (Ak-1[i, j], Ak-1[i, k] + Ak-1[k, j])
return A
Python, Java and C/C++ Examples
# Floyd Warshall Algorithm in python
# The number of vertices
nV = 4
INF = 999
# Algorithm implementation
def floyd_warshall(G):
distance = list(map(lambda i: list(map(lambda j: j, i)), G))
# Adding vertices individually
for k in range(nV):
for i in range(nV):
for j in range(nV):
distance[i][j] = min(distance[i][j], distance[i][k] + distance[k][j])
print_solution(distance)
# Printing the solution
def print_solution(distance):
for i in range(nV):
for j in range(nV):
if(distance[i][j] == INF):
print("INF", end=" ")
else:
print(distance[i][j], end=" ")
print(" ")
G = [[0, 3, INF, 5],
[2, 0, INF, 4],
[INF, 1, 0, INF],
[INF, INF, 2, 0]]
floyd_warshall(G)
// Floyd Warshall Algorithm in Java
class FloydWarshall {
final static int INF = 9999, nV = 4;
// Implementing floyd warshall algorithm
void floydWarshall(int graph[][]) {
int matrix[][] = new int[nV][nV];
int i, j, k;
for (i = 0; i < nV; i++)
for (j = 0; j < nV; j++)
matrix[i][j] = graph[i][j];
// Adding vertices individually
for (k = 0; k < nV; k++) {
for (i = 0; i < nV; i++) {
for (j = 0; j < nV; j++) {
if (matrix[i][k] + matrix[k][j] < matrix[i][j])
matrix[i][j] = matrix[i][k] + matrix[k][j];
}
}
}
printMatrix(matrix);
}
void printMatrix(int matrix[][]) {
for (int i = 0; i < nV; ++i) {
for (int j = 0; j < nV; ++j) {
if (matrix[i][j] == INF)
System.out.print("INF ");
else
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
int graph[][] = { { 0, 3, INF, 5 }, { 2, 0, INF, 4 }, { INF, 1, 0, INF }, { INF, INF, 2, 0 } };
FloydWarshall a = new FloydWarshall();
a.floydWarshall(graph);
}
}
// Floyd-Warshall Algorithm in C
#include <stdio.h>
// defining the number of vertices
#define nV 4
#define INF 999
void printMatrix(int matrix[][nV]);
// Implementing floyd warshall algorithm
void floydWarshall(int graph[][nV]) {
int matrix[nV][nV], i, j, k;
for (i = 0; i < nV; i++)
for (j = 0; j < nV; j++)
matrix[i][j] = graph[i][j];
// Adding vertices individually
for (k = 0; k < nV; k++) {
for (i = 0; i < nV; i++) {
for (j = 0; j < nV; j++) {
if (matrix[i][k] + matrix[k][j] < matrix[i][j])
matrix[i][j] = matrix[i][k] + matrix[k][j];
}
}
}
printMatrix(matrix);
}
void printMatrix(int matrix[][nV]) {
for (int i = 0; i < nV; i++) {
for (int j = 0; j < nV; j++) {
if (matrix[i][j] == INF)
printf("%4s", "INF");
else
printf("%4d", matrix[i][j]);
}
printf("\n");
}
}
int main() {
int graph[nV][nV] = {{0, 3, INF, 5},
{2, 0, INF, 4},
{INF, 1, 0, INF},
{INF, INF, 2, 0}};
floydWarshall(graph);
}
// Floyd-Warshall Algorithm in C++
#include <iostream>
using namespace std;
// defining the number of vertices
#define nV 4
#define INF 999
void printMatrix(int matrix[][nV]);
// Implementing floyd warshall algorithm
void floydWarshall(int graph[][nV]) {
int matrix[nV][nV], i, j, k;
for (i = 0; i < nV; i++)
for (j = 0; j < nV; j++)
matrix[i][j] = graph[i][j];
// Adding vertices individually
for (k = 0; k < nV; k++) {
for (i = 0; i < nV; i++) {
for (j = 0; j < nV; j++) {
if (matrix[i][k] + matrix[k][j] < matrix[i][j])
matrix[i][j] = matrix[i][k] + matrix[k][j];
}
}
}
printMatrix(matrix);
}
void printMatrix(int matrix[][nV]) {
for (int i = 0; i < nV; i++) {
for (int j = 0; j < nV; j++) {
if (matrix[i][j] == INF)
printf("%4s", "INF");
else
printf("%4d", matrix[i][j]);
}
printf("\n");
}
}
int main() {
int graph[nV][nV] = {{0, 3, INF, 5},
{2, 0, INF, 4},
{INF, 1, 0, INF},
{INF, INF, 2, 0}};
floydWarshall(graph);
}
Floyd Warshall Algorithm Complexity
Time Complexity
There are three loops. Each loop has constant complexities. So, the time complexity of the Floyd-Warshall algorithm is O(n3).
Space Complexity
The space complexity of the Floyd-Warshall algorithm is O(n2).
Floyd Warshall Algorithm Applications
- To find the shortest path is a directed graph
- To find the transitive closure of directed graphs
- To find the Inversion of real matrices
- For testing whether an undirected graph is bipartite