A strongly connected component is the portion of a directed graph in which there is a path from each vertex to another vertex. It is applicable only on a directed graph.
For example:
Let us take the graph below.
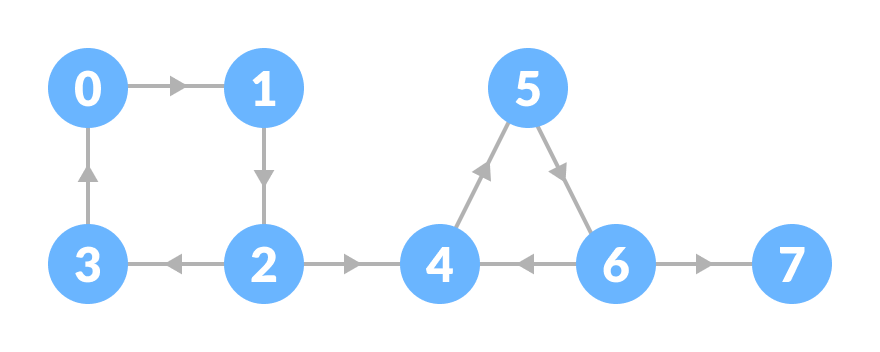
The strongly connected components of the above graph are:
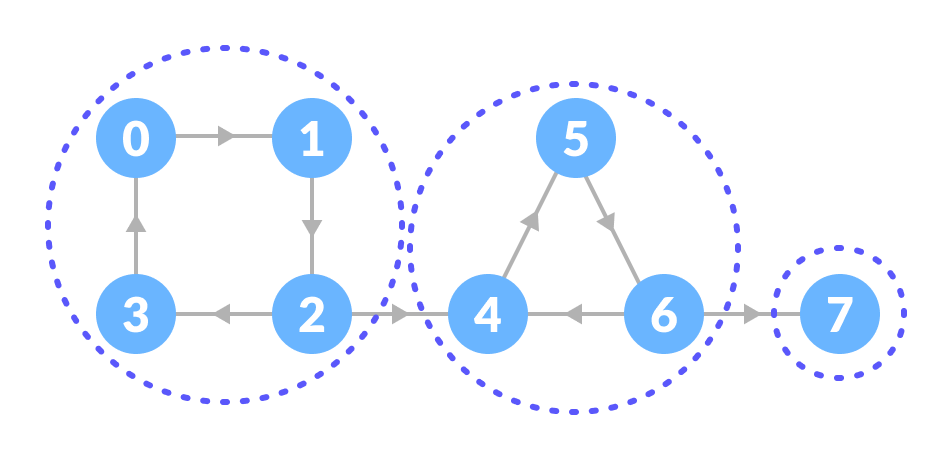
You can observe that in the first strongly connected component, every vertex can reach the other vertex through the directed path.
These components can be found using Kosaraju's Algorithm.
Kosaraju's Algorithm
Kosaraju's Algorithm is based on the depth-first search algorithm implemented twice.
Three steps are involved.
- Perform a depth first search on the whole graph.
Let us start from vertex-0, visit all of its child vertices, and mark the visited vertices as done. If a vertex leads to an already visited vertex, then push this vertex to the stack.
For example: Starting from vertex-0, go to vertex-1, vertex-2, and then to vertex-3. Vertex-3 leads to already visited vertex-0, so push the source vertex (ie. vertex-3) into the stack.
DFS on the graph
Go to the previous vertex (vertex-2) and visit its child vertices i.e. vertex-4, vertex-5, vertex-6 and vertex-7 sequentially. Since there is nowhere to go from vertex-7, push it into the stack.
DFS on the graph
Go to the previous vertex (vertex-6) and visit its child vertices. But, all of its child vertices are visited, so push it into the stack.
Stacking
Similarly, a final stack is created.
Final Stack - Reverse the original graph.

DFS on reversed graph - Perform depth-first search on the reversed graph.
Start from the top vertex of the stack. Traverse through all of its child vertices. Once the already visited vertex is reached, one strongly connected component is formed.
For example: Pop vertex-0 from the stack. Starting from vertex-0, traverse through its child vertices (vertex-0, vertex-1, vertex-2, vertex-3 in sequence) and mark them as visited. The child of vertex-3 is already visited, so these visited vertices form one strongly connected component.
Start from the top and traverse through all the vertices
Go to the stack and pop the top vertex if already visited. Otherwise, choose the top vertex from the stack and traverse through its child vertices as presented above.
Pop the top vertex if already visited 
Strongly connected component - Thus, the strongly connected components are:

All strongly connected components
Python, Java, C++ examples
# Kosaraju's algorithm to find strongly connected components in Python
from collections import defaultdict
class Graph:
def __init__(self, vertex):
self.V = vertex
self.graph = defaultdict(list)
# Add edge into the graph
def add_edge(self, s, d):
self.graph[s].append(d)
# dfs
def dfs(self, d, visited_vertex):
visited_vertex[d] = True
print(d, end='')
for i in self.graph[d]:
if not visited_vertex[i]:
self.dfs(i, visited_vertex)
def fill_order(self, d, visited_vertex, stack):
visited_vertex[d] = True
for i in self.graph[d]:
if not visited_vertex[i]:
self.fill_order(i, visited_vertex, stack)
stack = stack.append(d)
# transpose the matrix
def transpose(self):
g = Graph(self.V)
for i in self.graph:
for j in self.graph[i]:
g.add_edge(j, i)
return g
# Print stongly connected components
def print_scc(self):
stack = []
visited_vertex = [False] * (self.V)
for i in range(self.V):
if not visited_vertex[i]:
self.fill_order(i, visited_vertex, stack)
gr = self.transpose()
visited_vertex = [False] * (self.V)
while stack:
i = stack.pop()
if not visited_vertex[i]:
gr.dfs(i, visited_vertex)
print("")
g = Graph(8)
g.add_edge(0, 1)
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(2, 4)
g.add_edge(3, 0)
g.add_edge(4, 5)
g.add_edge(5, 6)
g.add_edge(6, 4)
g.add_edge(6, 7)
print("Strongly Connected Components:")
g.print_scc()
// Kosaraju's algorithm to find strongly connected components in Java
import java.util.*;
import java.util.LinkedList;
class Graph {
private int V;
private LinkedList<Integer> adj[];
// Create a graph
Graph(int s) {
V = s;
adj = new LinkedList[s];
for (int i = 0; i < s; ++i)
adj[i] = new LinkedList();
}
// Add edge
void addEdge(int s, int d) {
adj[s].add(d);
}
// DFS
void DFSUtil(int s, boolean visitedVertices[]) {
visitedVertices[s] = true;
System.out.print(s + " ");
int n;
Iterator<Integer> i = adj[s].iterator();
while (i.hasNext()) {
n = i.next();
if (!visitedVertices[n])
DFSUtil(n, visitedVertices);
}
}
// Transpose the graph
Graph Transpose() {
Graph g = new Graph(V);
for (int s = 0; s < V; s++) {
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext())
g.adj[i.next()].add(s);
}
return g;
}
void fillOrder(int s, boolean visitedVertices[], Stack stack) {
visitedVertices[s] = true;
Iterator<Integer> i = adj[s].iterator();
while (i.hasNext()) {
int n = i.next();
if (!visitedVertices[n])
fillOrder(n, visitedVertices, stack);
}
stack.push(new Integer(s));
}
// Print strongly connected component
void printSCC() {
Stack stack = new Stack();
boolean visitedVertices[] = new boolean[V];
for (int i = 0; i < V; i++)
visitedVertices[i] = false;
for (int i = 0; i < V; i++)
if (visitedVertices[i] == false)
fillOrder(i, visitedVertices, stack);
Graph gr = Transpose();
for (int i = 0; i < V; i++)
visitedVertices[i] = false;
while (stack.empty() == false) {
int s = (int) stack.pop();
if (visitedVertices[s] == false) {
gr.DFSUtil(s, visitedVertices);
System.out.println();
}
}
}
public static void main(String args[]) {
Graph g = new Graph(8);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 3);
g.addEdge(2, 4);
g.addEdge(3, 0);
g.addEdge(4, 5);
g.addEdge(5, 6);
g.addEdge(6, 4);
g.addEdge(6, 7);
System.out.println("Strongly Connected Components:");
g.printSCC();
}
}
// Kosaraju's algorithm to find strongly connected components in C++
#include <iostream>
#include <list>
#include <stack>
using namespace std;
class Graph {
int V;
list<int> *adj;
void fillOrder(int s, bool visitedV[], stack<int> &Stack);
void DFS(int s, bool visitedV[]);
public:
Graph(int V);
void addEdge(int s, int d);
void printSCC();
Graph transpose();
};
Graph::Graph(int V) {
this->V = V;
adj = new list<int>[V];
}
// DFS
void Graph::DFS(int s, bool visitedV[]) {
visitedV[s] = true;
cout << s << " ";
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i)
if (!visitedV[*i])
DFS(*i, visitedV);
}
// Transpose
Graph Graph::transpose() {
Graph g(V);
for (int s = 0; s < V; s++) {
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i) {
g.adj[*i].push_back(s);
}
}
return g;
}
// Add edge into the graph
void Graph::addEdge(int s, int d) {
adj[s].push_back(d);
}
void Graph::fillOrder(int s, bool visitedV[], stack<int> &Stack) {
visitedV[s] = true;
list<int>::iterator i;
for (i = adj[s].begin(); i != adj[s].end(); ++i)
if (!visitedV[*i])
fillOrder(*i, visitedV, Stack);
Stack.push(s);
}
// Print strongly connected component
void Graph::printSCC() {
stack<int> Stack;
bool *visitedV = new bool[V];
for (int i = 0; i < V; i++)
visitedV[i] = false;
for (int i = 0; i < V; i++)
if (visitedV[i] == false)
fillOrder(i, visitedV, Stack);
Graph gr = transpose();
for (int i = 0; i < V; i++)
visitedV[i] = false;
while (Stack.empty() == false) {
int s = Stack.top();
Stack.pop();
if (visitedV[s] == false) {
gr.DFS(s, visitedV);
cout << endl;
}
}
}
int main() {
Graph g(8);
g.addEdge(0, 1);
g.addEdge(1, 2);
g.addEdge(2, 3);
g.addEdge(2, 4);
g.addEdge(3, 0);
g.addEdge(4, 5);
g.addEdge(5, 6);
g.addEdge(6, 4);
g.addEdge(6, 7);
cout << "Strongly Connected Components:\n";
g.printSCC();
}
Kosaraju's Algorithm Complexity
Kosaraju's algorithm runs in linear time i.e. O(V+E).
Strongly Connected Components Applications
- Vehicle routing applications
- Maps
- Model-checking in formal verification









