Traversal means visiting all the nodes of a graph. Breadth First Traversal or Breadth First Search is a recursive algorithm for searching all the vertices of a graph or tree data structure.
BFS algorithm
A standard BFS implementation puts each vertex of the graph into one of two categories:
- Visited
- Not Visited
The purpose of the algorithm is to mark each vertex as visited while avoiding cycles.
The algorithm works as follows:
- Start by putting any one of the graph's vertices at the back of a queue.
- Take the front item of the queue and add it to the visited list.
- Create a list of that vertex's adjacent nodes. Add the ones which aren't in the visited list to the back of the queue.
- Keep repeating steps 2 and 3 until the queue is empty.
The graph might have two different disconnected parts so to make sure that we cover every vertex, we can also run the BFS algorithm on every node
BFS example
Let's see how the Breadth First Search algorithm works with an example. We use an undirected graph with 5 vertices.

We start from vertex 0, the BFS algorithm starts by putting it in the Visited list and putting all its adjacent vertices in the queue.
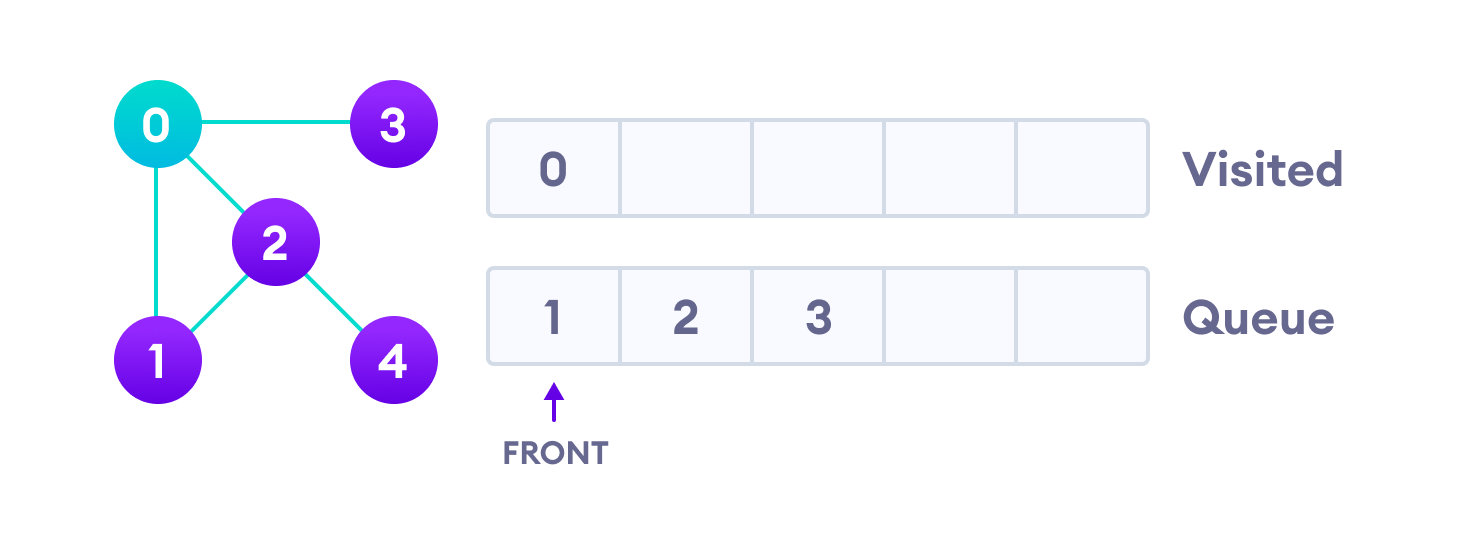
Next, we visit the element at the front of queue i.e. 1 and go to its adjacent nodes. Since 0 has already been visited, we visit 2 instead.
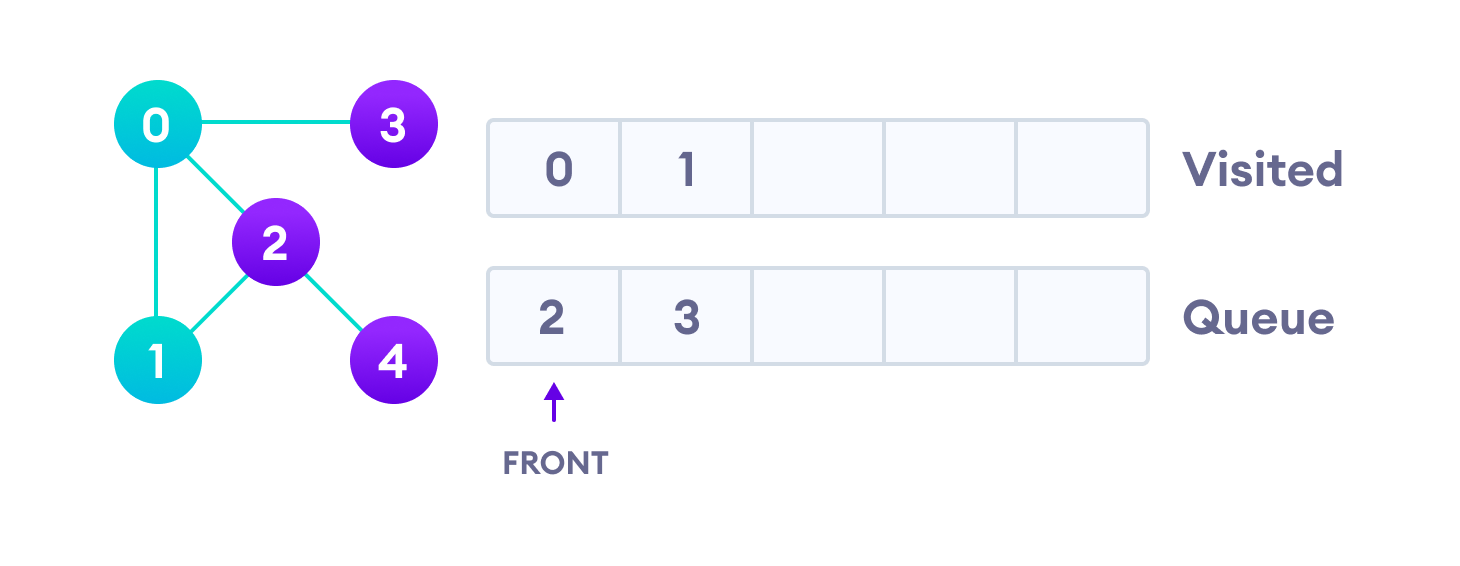
Vertex 2 has an unvisited adjacent vertex in 4, so we add that to the back of the queue and visit 3, which is at the front of the queue.
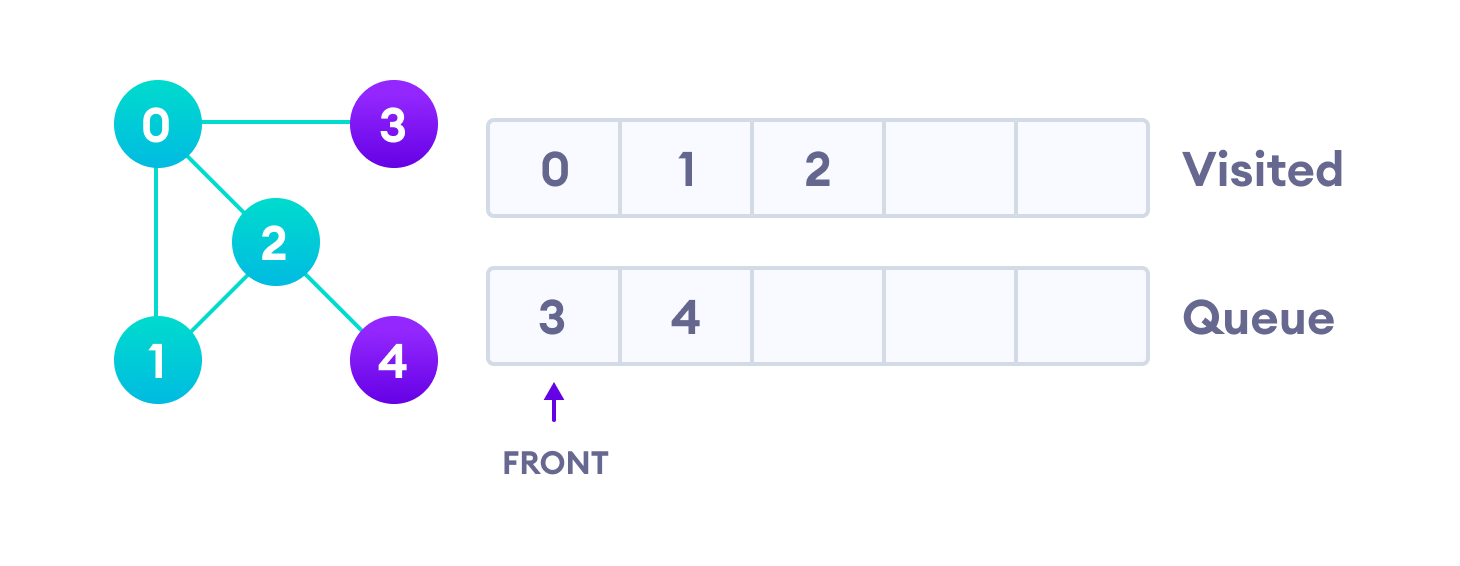
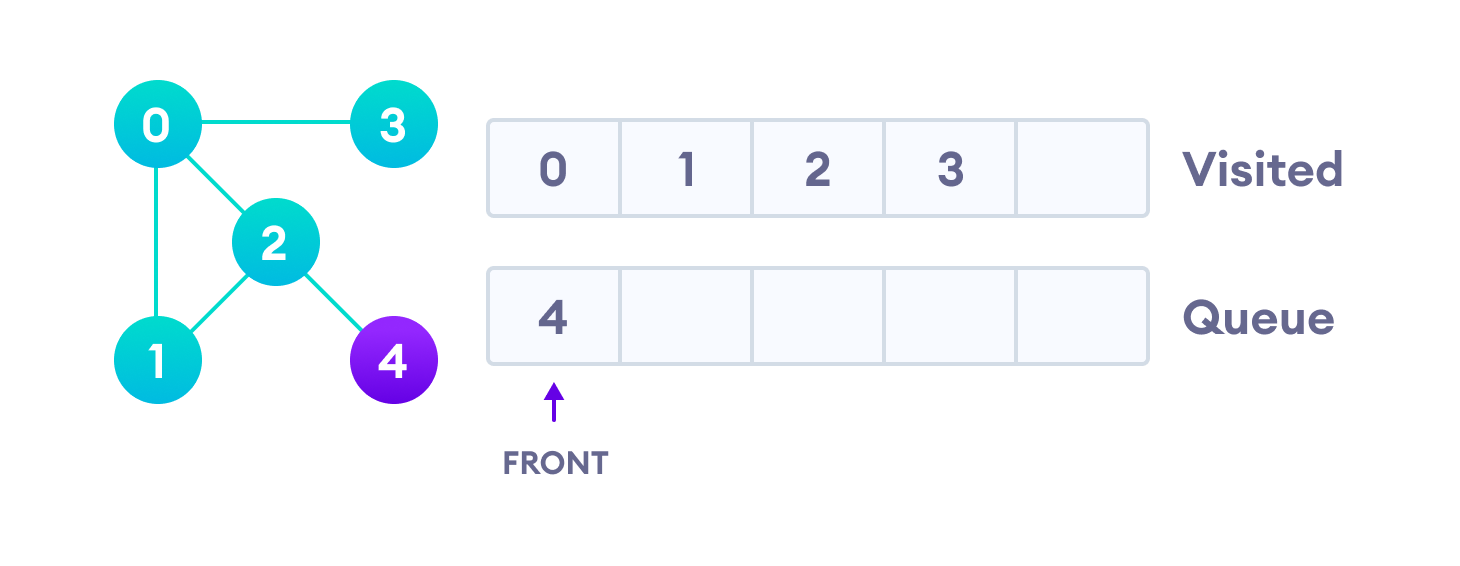
Only 4 remains in the queue since the only adjacent node of 3 i.e. 0 is already visited. We visit it.
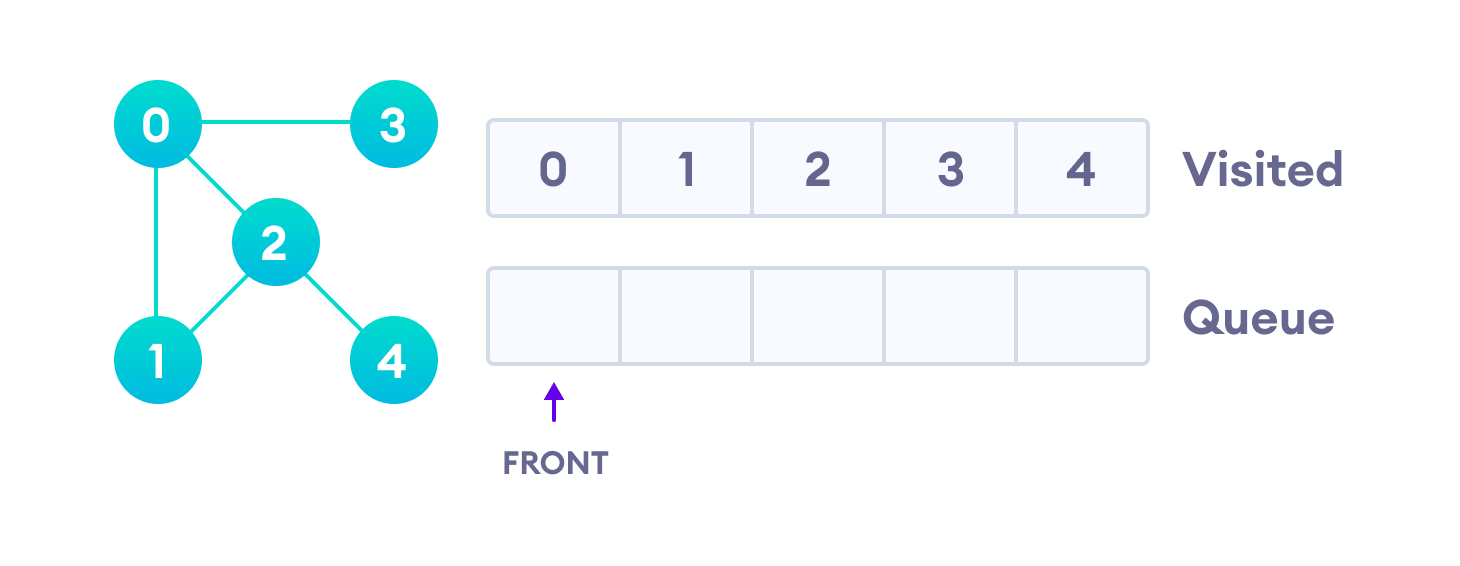
Since the queue is empty, we have completed the Breadth First Traversal of the graph.
BFS pseudocode
create a queue Q
mark v as visited and put v into Q
while Q is non-empty
remove the head u of Q
mark and enqueue all (unvisited) neighbours of u
Python, Java and C/C++ Examples
The code for the Breadth First Search Algorithm with an example is shown below. The code has been simplified so that we can focus on the algorithm rather than other details.
# BFS algorithm in Python
import collections
# BFS algorithm
def bfs(graph, root):
visited, queue = set(), collections.deque([root])
visited.add(root)
while queue:
# Dequeue a vertex from queue
vertex = queue.popleft()
print(str(vertex) + " ", end="")
# If not visited, mark it as visited, and
# enqueue it
for neighbour in graph[vertex]:
if neighbour not in visited:
visited.add(neighbour)
queue.append(neighbour)
if __name__ == '__main__':
graph = {0: [1, 2], 1: [2], 2: [3], 3: [1, 2]}
print("Following is Breadth First Traversal: ")
bfs(graph, 0)
// BFS algorithm in Java
import java.util.*;
public class Graph {
private int V;
private LinkedList<Integer> adj[];
// Create a graph
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i)
adj[i] = new LinkedList();
}
// Add edges to the graph
void addEdge(int v, int w) {
adj[v].add(w);
}
// BFS algorithm
void BFS(int s) {
boolean visited[] = new boolean[V];
LinkedList<Integer> queue = new LinkedList();
visited[s] = true;
queue.add(s);
while (queue.size() != 0) {
s = queue.poll();
System.out.print(s + " ");
Iterator<Integer> i = adj[s].listIterator();
while (i.hasNext()) {
int n = i.next();
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
public static void main(String args[]) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
System.out.println("Following is Breadth First Traversal " + "(starting from vertex 2)");
g.BFS(2);
}
}
// BFS algorithm in C
#include <stdio.h>
#include <stdlib.h>
#define SIZE 40
struct queue {
int items[SIZE];
int front;
int rear;
};
struct queue* createQueue();
void enqueue(struct queue* q, int);
int dequeue(struct queue* q);
void display(struct queue* q);
int isEmpty(struct queue* q);
void printQueue(struct queue* q);
struct node {
int vertex;
struct node* next;
};
struct node* createNode(int);
struct Graph {
int numVertices;
struct node** adjLists;
int* visited;
};
// BFS algorithm
void bfs(struct Graph* graph, int startVertex) {
struct queue* q = createQueue();
graph->visited[startVertex] = 1;
enqueue(q, startVertex);
while (!isEmpty(q)) {
printQueue(q);
int currentVertex = dequeue(q);
printf("Visited %d\n", currentVertex);
struct node* temp = graph->adjLists[currentVertex];
while (temp) {
int adjVertex = temp->vertex;
if (graph->visited[adjVertex] == 0) {
graph->visited[adjVertex] = 1;
enqueue(q, adjVertex);
}
temp = temp->next;
}
}
}
// Creating a node
struct node* createNode(int v) {
struct node* newNode = malloc(sizeof(struct node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// Creating a graph
struct Graph* createGraph(int vertices) {
struct Graph* graph = malloc(sizeof(struct Graph));
graph->numVertices = vertices;
graph->adjLists = malloc(vertices * sizeof(struct node*));
graph->visited = malloc(vertices * sizeof(int));
int i;
for (i = 0; i < vertices; i++) {
graph->adjLists[i] = NULL;
graph->visited[i] = 0;
}
return graph;
}
// Add edge
void addEdge(struct Graph* graph, int src, int dest) {
// Add edge from src to dest
struct node* newNode = createNode(dest);
newNode->next = graph->adjLists[src];
graph->adjLists[src] = newNode;
// Add edge from dest to src
newNode = createNode(src);
newNode->next = graph->adjLists[dest];
graph->adjLists[dest] = newNode;
}
// Create a queue
struct queue* createQueue() {
struct queue* q = malloc(sizeof(struct queue));
q->front = -1;
q->rear = -1;
return q;
}
// Check if the queue is empty
int isEmpty(struct queue* q) {
if (q->rear == -1)
return 1;
else
return 0;
}
// Adding elements into queue
void enqueue(struct queue* q, int value) {
if (q->rear == SIZE - 1)
printf("\nQueue is Full!!");
else {
if (q->front == -1)
q->front = 0;
q->rear++;
q->items[q->rear] = value;
}
}
// Removing elements from queue
int dequeue(struct queue* q) {
int item;
if (isEmpty(q)) {
printf("Queue is empty");
item = -1;
} else {
item = q->items[q->front];
q->front++;
if (q->front > q->rear) {
printf("Resetting queue ");
q->front = q->rear = -1;
}
}
return item;
}
// Print the queue
void printQueue(struct queue* q) {
int i = q->front;
if (isEmpty(q)) {
printf("Queue is empty");
} else {
printf("\nQueue contains \n");
for (i = q->front; i < q->rear + 1; i++) {
printf("%d ", q->items[i]);
}
}
}
int main() {
struct Graph* graph = createGraph(6);
addEdge(graph, 0, 1);
addEdge(graph, 0, 2);
addEdge(graph, 1, 2);
addEdge(graph, 1, 4);
addEdge(graph, 1, 3);
addEdge(graph, 2, 4);
addEdge(graph, 3, 4);
bfs(graph, 0);
return 0;
}
// BFS algorithm in C++
#include <iostream>
#include <list>
using namespace std;
class Graph {
int numVertices;
list<int>* adjLists;
bool* visited;
public:
Graph(int vertices);
void addEdge(int src, int dest);
void BFS(int startVertex);
};
// Create a graph with given vertices,
// and maintain an adjacency list
Graph::Graph(int vertices) {
numVertices = vertices;
adjLists = new list<int>[vertices];
}
// Add edges to the graph
void Graph::addEdge(int src, int dest) {
adjLists[src].push_back(dest);
adjLists[dest].push_back(src);
}
// BFS algorithm
void Graph::BFS(int startVertex) {
visited = new bool[numVertices];
for (int i = 0; i < numVertices; i++)
visited[i] = false;
list<int> queue;
visited[startVertex] = true;
queue.push_back(startVertex);
list<int>::iterator i;
while (!queue.empty()) {
int currVertex = queue.front();
cout << "Visited " << currVertex << " ";
queue.pop_front();
for (i = adjLists[currVertex].begin(); i != adjLists[currVertex].end(); ++i) {
int adjVertex = *i;
if (!visited[adjVertex]) {
visited[adjVertex] = true;
queue.push_back(adjVertex);
}
}
}
}
int main() {
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);
g.BFS(2);
return 0;
}
BFS Algorithm Complexity
The time complexity of the BFS algorithm is represented in the form of O(V + E), where V is the number of nodes and E is the number of edges.
The space complexity of the algorithm is O(V).
BFS Algorithm Applications
- To build index by search index
- For GPS navigation
- Path finding algorithms
- In Ford-Fulkerson algorithm to find maximum flow in a network
- Cycle detection in an undirected graph
- In minimum spanning tree
