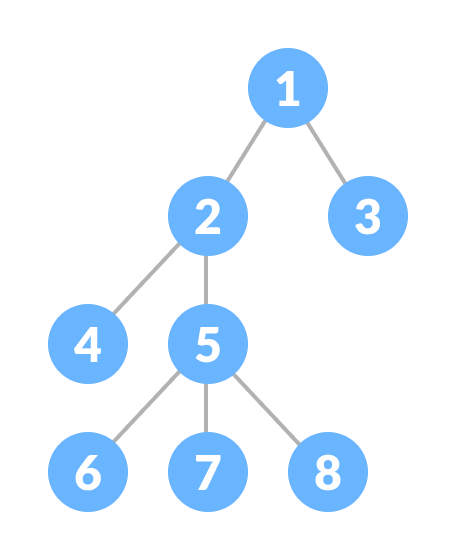
A tree is a nonlinear hierarchical data structure that consists of nodes connected by edges.
Why Tree Data Structure?
Other data structures such as arrays, linked list, stack, and queue are linear data structures that store data sequentially. In order to perform any operation in a linear data structure, the time complexity increases with the increase in the data size. But, it is not acceptable in today's computational world.
Different tree data structures allow quicker and easier access to the data as it is a non-linear data structure.
Tree Terminologies
Node
A node is an entity that contains a key or value and pointers to its child nodes.
The last nodes of each path are called leaf nodes or external nodes that do not contain a link/pointer to child nodes.
The node having at least a child node is called an internal node.
Edge
It is the link between any two nodes.

Root
It is the topmost node of a tree.
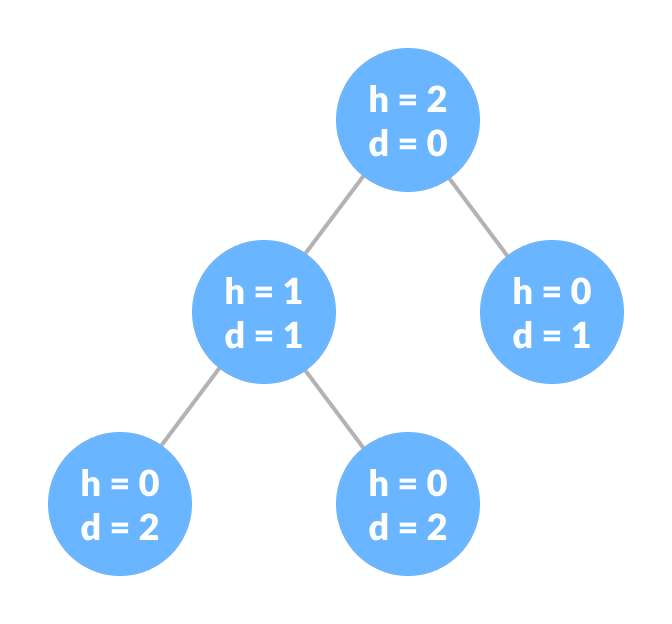
Height of a Node
The height of a node is the number of edges from the node to the deepest leaf (ie. the longest path from the node to a leaf node).
Depth of a Node
The depth of a node is the number of edges from the root to the node.
Height of a Tree
The height of a Tree is the height of the root node or the depth of the deepest node.
Degree of a Node
The degree of a node is the total number of branches of that node.
Forest
A collection of disjoint trees is called a forest.

You can create a forest by cutting the root of a tree.
Types of Tree
Tree Traversal
In order to perform any operation on a tree, you need to reach to the specific node. The tree traversal algorithm helps in visiting a required node in the tree.
To learn more, please visit tree traversal.
Tree Applications
- Binary Search Trees(BSTs) are used to quickly check whether an element is present in a set or not.
- Heap is a kind of tree that is used for heap sort.
- A modified version of a tree called Tries is used in modern routers to store routing information.
- Most popular databases use B-Trees and T-Trees, which are variants of the tree structure we learned above to store their data
- Compilers use a syntax tree to validate the syntax of every program you write.
