An adjacency matrix is a way of representing a graph as a matrix of booleans (0's and 1's). A finite graph can be represented in the form of a square matrix on a computer, where the boolean value of the matrix indicates if there is a direct path between two vertices.
For example, we have a graph below.
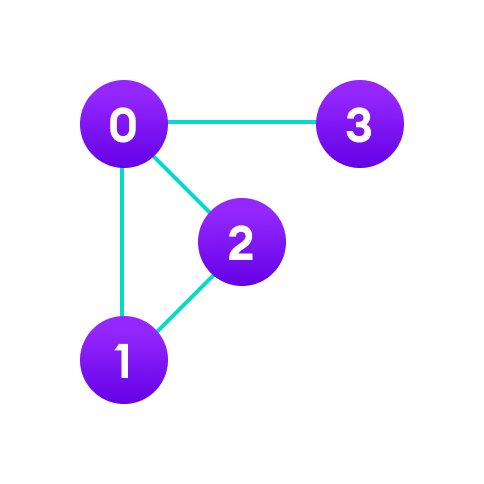
We can represent this graph in matrix form like below.
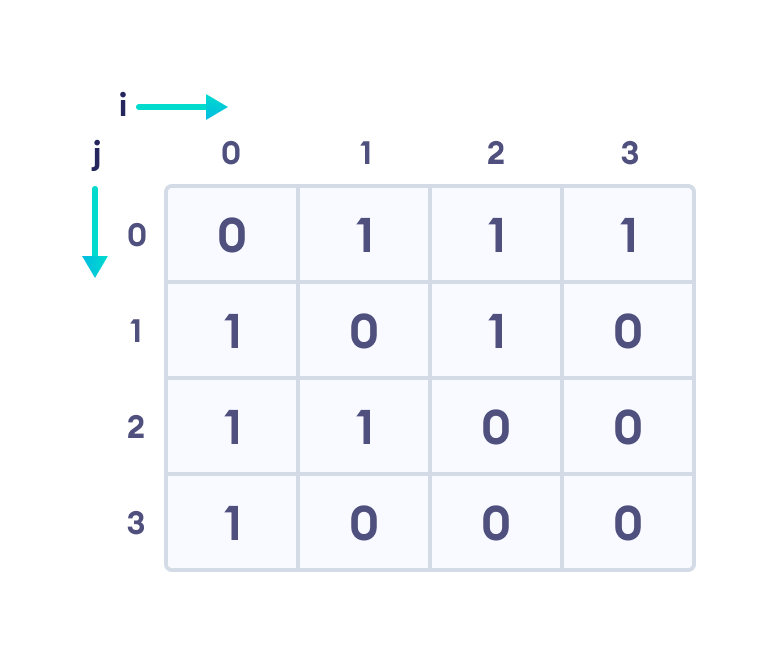
Each cell in the above table/matrix is represented as Aij, where i and j are vertices. The value of Aij is either 1 or 0 depending on whether there is an edge from vertex i to vertex j.
If there is a path from i to j, then the value of Aij is 1 otherwise its 0. For instance, there is a path from vertex 1 to vertex 2, so A12 is 1 and there is no path from vertex 1 to 3, so A13 is 0.
In case of undirected graphs, the matrix is symmetric about the diagonal because of every edge (i,j), there is also an edge (j,i).
Pros of Adjacency Matrix
- The basic operations like adding an edge, removing an edge, and checking whether there is an edge from vertex i to vertex j are extremely time efficient, constant time operations.
- If the graph is dense and the number of edges is large, an adjacency matrix should be the first choice. Even if the graph and the adjacency matrix is sparse, we can represent it using data structures for sparse matrices.
- The biggest advantage, however, comes from the use of matrices. The recent advances in hardware enable us to perform even expensive matrix operations on the GPU.
- By performing operations on the adjacent matrix, we can get important insights into the nature of the graph and the relationship between its vertices.
Cons of Adjacency Matrix
- The
VxVspace requirement of the adjacency matrix makes it a memory hog. Graphs out in the wild usually don't have too many connections and this is the major reason why adjacency lists are the better choice for most tasks. - While basic operations are easy, operations like
inEdgesandoutEdgesare expensive when using the adjacency matrix representation.
Adjacency Matrix Code in Python, Java, and C/C++
If you know how to create two-dimensional arrays, you also know how to create an adjacency matrix.
# Adjacency Matrix representation in Python
class Graph(object):
# Initialize the matrix
def __init__(self, size):
self.adjMatrix = []
for i in range(size):
self.adjMatrix.append([0 for i in range(size)])
self.size = size
# Add edges
def add_edge(self, v1, v2):
if v1 == v2:
print("Same vertex %d and %d" % (v1, v2))
self.adjMatrix[v1][v2] = 1
self.adjMatrix[v2][v1] = 1
# Remove edges
def remove_edge(self, v1, v2):
if self.adjMatrix[v1][v2] == 0:
print("No edge between %d and %d" % (v1, v2))
return
self.adjMatrix[v1][v2] = 0
self.adjMatrix[v2][v1] = 0
def __len__(self):
return self.size
# Print the matrix
def print_matrix(self):
for row in self.adjMatrix:
for val in row:
print('{:4}'.format(val)),
print
def main():
g = Graph(5)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 0)
g.add_edge(2, 3)
g.print_matrix()
if __name__ == '__main__':
main()
// Adjacency Matrix representation in Java
public class Graph {
private boolean adjMatrix[][];
private int numVertices;
// Initialize the matrix
public Graph(int numVertices) {
this.numVertices = numVertices;
adjMatrix = new boolean[numVertices][numVertices];
}
// Add edges
public void addEdge(int i, int j) {
adjMatrix[i][j] = true;
adjMatrix[j][i] = true;
}
// Remove edges
public void removeEdge(int i, int j) {
adjMatrix[i][j] = false;
adjMatrix[j][i] = false;
}
// Print the matrix
public String toString() {
StringBuilder s = new StringBuilder();
for (int i = 0; i < numVertices; i++) {
s.append(i + ": ");
for (boolean j : adjMatrix[i]) {
s.append((j ? 1 : 0) + " ");
}
s.append("\n");
}
return s.toString();
}
public static void main(String args[]) {
Graph g = new Graph(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
System.out.print(g.toString());
}
}
// Adjacency Matrix representation in C
#include <stdio.h>
#define V 4
// Initialize the matrix to zero
void init(int arr[][V]) {
int i, j;
for (i = 0; i < V; i++)
for (j = 0; j < V; j++)
arr[i][j] = 0;
}
// Add edges
void addEdge(int arr[][V], int i, int j) {
arr[i][j] = 1;
arr[j][i] = 1;
}
// Print the matrix
void printAdjMatrix(int arr[][V]) {
int i, j;
for (i = 0; i < V; i++) {
printf("%d: ", i);
for (j = 0; j < V; j++) {
printf("%d ", arr[i][j]);
}
printf("\n");
}
}
int main() {
int adjMatrix[V][V];
init(adjMatrix);
addEdge(adjMatrix, 0, 1);
addEdge(adjMatrix, 0, 2);
addEdge(adjMatrix, 1, 2);
addEdge(adjMatrix, 2, 0);
addEdge(adjMatrix, 2, 3);
printAdjMatrix(adjMatrix);
return 0;
}
// Adjacency Matrix representation in C++
#include <iostream>
using namespace std;
class Graph {
private:
bool** adjMatrix;
int numVertices;
public:
// Initialize the matrix to zero
Graph(int numVertices) {
this->numVertices = numVertices;
adjMatrix = new bool*[numVertices];
for (int i = 0; i < numVertices; i++) {
adjMatrix[i] = new bool[numVertices];
for (int j = 0; j < numVertices; j++)
adjMatrix[i][j] = false;
}
}
// Add edges
void addEdge(int i, int j) {
adjMatrix[i][j] = true;
adjMatrix[j][i] = true;
}
// Remove edges
void removeEdge(int i, int j) {
adjMatrix[i][j] = false;
adjMatrix[j][i] = false;
}
// Print the martix
void toString() {
for (int i = 0; i < numVertices; i++) {
cout << i << " : ";
for (int j = 0; j < numVertices; j++)
cout << adjMatrix[i][j] << " ";
cout << "\n";
}
}
~Graph() {
for (int i = 0; i < numVertices; i++)
delete[] adjMatrix[i];
delete[] adjMatrix;
}
};
int main() {
Graph g(4);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.toString();
}
Adjacency Matrix Applications
- Creating routing table in networks
- Navigation tasks
