The longest common subsequence (LCS) is defined as the longest subsequence that is common to all the given sequences, provided that the elements of the subsequence are not required to occupy consecutive positions within the original sequences.
If S1 and S2 are the two given sequences then, Z is the common subsequence of S1 and S2 if Z is a subsequence of both S1 and S2. Furthermore, Z must be a strictly increasing sequence of the indices of both S1 and S2.
In a strictly increasing sequence, the indices of the elements chosen from the original sequences must be in ascending order in Z.
If
S1 = {B, C, D, A, A, C, D}
Then, {A, D, B} cannot be a subsequence of S1 as the order of the elements is not the same (ie. not strictly increasing sequence).
Let us understand LCS with an example.
If
S1 = {B, C, D, A, A, C, D}
S2 = {A, C, D, B, A, C}
A subsequence is a sequence derived by deleting some or no elements from the original sequence without changing the order of the remaining elements. A common subsequence means a subsequence that appears in both sequences in the same relative order.
Here, common subsequences are {B, C}, {C, D, A, C}, {D, A, C}, {A, A, C}, {A, C}, {C, D}, ...
Among these subsequences, {C, D, A, C} is the longest common subsequence. We are going to find this longest common subsequence using dynamic programming.
Before proceeding further, if you do not already know about dynamic programming, please go through dynamic programming.
Using Dynamic Programming to find the LCS
Let us take two sequences:


The following steps are followed for finding the longest common subsequence.
- Create a table of dimension
n+1*m+1where n and m are the lengths of X and Y respectively. The first row and the first column are filled with zeros.
Initialise a table - Fill each cell of the table using the following logic.
- If the character correspoding to the current row and current column are matching, then fill the current cell by adding one to the diagonal element. Point an arrow to the diagonal cell.
- Else take the maximum value from the previous column and previous row element for filling the current cell. Point an arrow to the cell with maximum value. If they are equal, point to any of them.
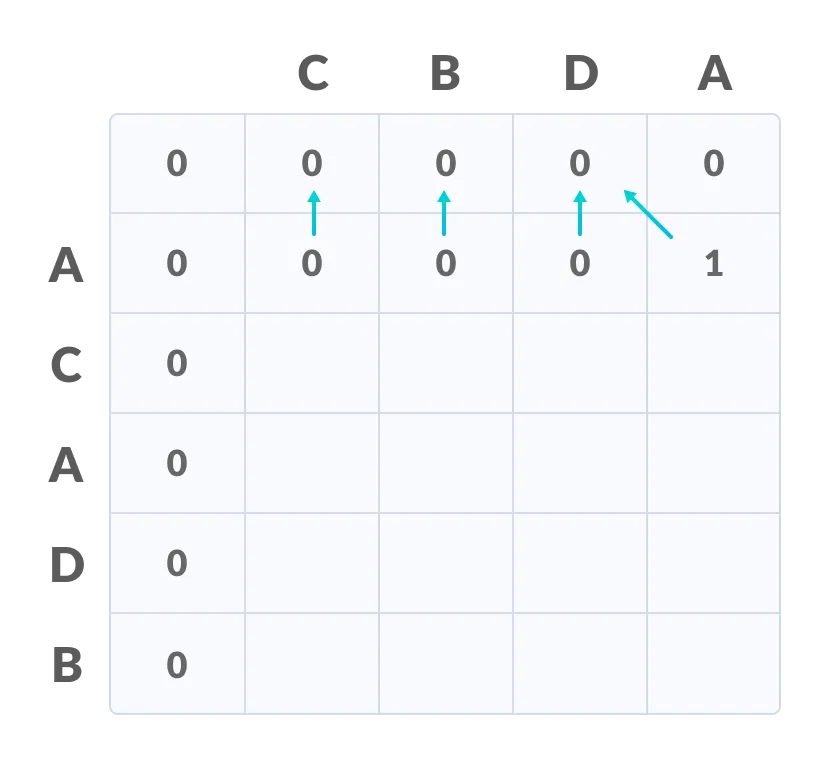
Fill the values - Step 2 is repeated until the table is filled.

Fill all the values - The value in the last row and the last column is the length of the longest common subsequence.

The bottom right corner is the length of the LCS - In order to find the longest common subsequence, start from the last element and follow the direction of the arrow. The elements corresponding to () symbol form the longest common subsequence.

Create a path according to the arrows
Thus, the longest common subsequence is CA.

How is a dynamic programming algorithm more efficient than the recursive algorithm while solving an LCS problem?
The method of dynamic programming reduces the number of function calls. It stores the result of each function call so that it can be used in future calls without the need for redundant calls.
In the above dynamic algorithm, the results obtained from each comparison between elements of X and the elements of Y are stored in a table so that they can be used in future computations.
So, the time taken by a dynamic approach is the time taken to fill the table (ie. O(mn)). Whereas, the recursion algorithm has the complexity of 2max(m, n).
Longest Common Subsequence Algorithm
X and Y be two given sequences
Initialize a table LCS of dimension X.length * Y.length
X.label = X
Y.label = Y
LCS[0][] = 0
LCS[][0] = 0
Start from LCS[1][1]
Compare X[i] and Y[j]
If X[i] = Y[j]
LCS[i][j] = 1 + LCS[i-1, j-1]
Point an arrow to LCS[i][j]
Else
LCS[i][j] = max(LCS[i-1][j], LCS[i][j-1])
Point an arrow to max(LCS[i-1][j], LCS[i][j-1])
Python, Java and C/C++ Examples
# The longest common subsequence in Python
# Function to find lcs_algo
def lcs_algo(S1, S2, m, n):
L = [[0 for x in range(n+1)] for x in range(m+1)]
# Building the mtrix in bottom-up way
for i in range(m+1):
for j in range(n+1):
if i == 0 or j == 0:
L[i][j] = 0
elif S1[i-1] == S2[j-1]:
L[i][j] = L[i-1][j-1] + 1
else:
L[i][j] = max(L[i-1][j], L[i][j-1])
index = L[m][n]
lcs_algo = [""] * (index+1)
lcs_algo[index] = ""
i = m
j = n
while i > 0 and j > 0:
if S1[i-1] == S2[j-1]:
lcs_algo[index-1] = S1[i-1]
i -= 1
j -= 1
index -= 1
elif L[i-1][j] > L[i][j-1]:
i -= 1
else:
j -= 1
# Printing the sub sequences
print("S1 : " + S1 + "\nS2 : " + S2)
print("LCS: " + "".join(lcs_algo))
S1 = "ACADB"
S2 = "CBDA"
m = len(S1)
n = len(S2)
lcs_algo(S1, S2, m, n)
// The longest common subsequence in Java
class LCS_ALGO {
static void lcs(String S1, String S2, int m, int n) {
int[][] LCS_table = new int[m + 1][n + 1];
// Building the mtrix in bottom-up way
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
LCS_table[i][j] = 0;
else if (S1.charAt(i - 1) == S2.charAt(j - 1))
LCS_table[i][j] = LCS_table[i - 1][j - 1] + 1;
else
LCS_table[i][j] = Math.max(LCS_table[i - 1][j], LCS_table[i][j - 1]);
}
}
int index = LCS_table[m][n];
int temp = index;
char[] lcs = new char[index + 1];
lcs[index] = '\0';
int i = m, j = n;
while (i > 0 && j > 0) {
if (S1.charAt(i - 1) == S2.charAt(j - 1)) {
lcs[index - 1] = S1.charAt(i - 1);
i--;
j--;
index--;
}
else if (LCS_table[i - 1][j] > LCS_table[i][j - 1])
i--;
else
j--;
}
// Printing the sub sequences
System.out.print("S1 : " + S1 + "\nS2 : " + S2 + "\nLCS: ");
for (int k = 0; k <= temp; k++)
System.out.print(lcs[k]);
System.out.println("");
}
public static void main(String[] args) {
String S1 = "ACADB";
String S2 = "CBDA";
int m = S1.length();
int n = S2.length();
lcs(S1, S2, m, n);
}
}
// The longest common subsequence in C
#include <stdio.h>
#include <string.h>
int i, j, m, n, LCS_table[20][20];
char S1[20] = "ACADB", S2[20] = "CBDA", b[20][20];
void lcsAlgo() {
m = strlen(S1);
n = strlen(S2);
// Filling 0's in the matrix
for (i = 0; i <= m; i++)
LCS_table[i][0] = 0;
for (i = 0; i <= n; i++)
LCS_table[0][i] = 0;
// Building the mtrix in bottom-up way
for (i = 1; i <= m; i++)
for (j = 1; j <= n; j++) {
if (S1[i - 1] == S2[j - 1]) {
LCS_table[i][j] = LCS_table[i - 1][j - 1] + 1;
} else if (LCS_table[i - 1][j] >= LCS_table[i][j - 1]) {
LCS_table[i][j] = LCS_table[i - 1][j];
} else {
LCS_table[i][j] = LCS_table[i][j - 1];
}
}
int index = LCS_table[m][n];
char lcsAlgo[index + 1];
lcsAlgo[index] = '\0';
int i = m, j = n;
while (i > 0 && j > 0) {
if (S1[i - 1] == S2[j - 1]) {
lcsAlgo[index - 1] = S1[i - 1];
i--;
j--;
index--;
}
else if (LCS_table[i - 1][j] > LCS_table[i][j - 1])
i--;
else
j--;
}
// Printing the sub sequences
printf("S1 : %s \nS2 : %s \n", S1, S2);
printf("LCS: %s", lcsAlgo);
}
int main() {
lcsAlgo();
printf("\n");
}
// The longest common subsequence in C++
#include <iostream>
using namespace std;
void lcsAlgo(char *S1, char *S2, int m, int n) {
int LCS_table[m + 1][n + 1];
// Building the mtrix in bottom-up way
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
LCS_table[i][j] = 0;
else if (S1[i - 1] == S2[j - 1])
LCS_table[i][j] = LCS_table[i - 1][j - 1] + 1;
else
LCS_table[i][j] = max(LCS_table[i - 1][j], LCS_table[i][j - 1]);
}
}
int index = LCS_table[m][n];
char lcsAlgo[index + 1];
lcsAlgo[index] = '\0';
int i = m, j = n;
while (i > 0 && j > 0) {
if (S1[i - 1] == S2[j - 1]) {
lcsAlgo[index - 1] = S1[i - 1];
i--;
j--;
index--;
}
else if (LCS_table[i - 1][j] > LCS_table[i][j - 1])
i--;
else
j--;
}
// Printing the sub sequences
cout << "S1 : " << S1 << "\nS2 : " << S2 << "\nLCS: " << lcsAlgo << "\n";
}
int main() {
char S1[] = "ACADB";
char S2[] = "CBDA";
int m = strlen(S1);
int n = strlen(S2);
lcsAlgo(S1, S2, m, n);
}
Longest Common Subsequence Applications
- in compressing genome resequencing data
- to authenticate users within their mobile phone through in-air signatures





