Shell sort is a generalized version of the insertion sort algorithm. It first sorts elements that are far apart from each other and successively reduces the interval between the elements to be sorted.
The interval between the elements is reduced based on the sequence used. Some of the optimal sequences that can be used in the shell sort algorithm are:
- Shell's original sequence:
N/2 , N/4 , …, 1 - Knuth's increments:
1, 4, 13, …, (3k– 1) / 2 - Sedgewick's increments:
1, 8, 23, 77, 281, 1073, 4193, 16577...4j+1+ 3·2j+ 1 - Hibbard's increments:
1, 3, 7, 15, 31, 63, 127, 255, 511… - Papernov & Stasevich increment:
1, 3, 5, 9, 17, 33, 65,... - Pratt:
1, 2, 3, 4, 6, 9, 8, 12, 18, 27, 16, 24, 36, 54, 81....
Note: The performance of the shell sort depends on the type of sequence used for a given input array.
Working of Shell Sort
- Suppose, we need to sort the following array.

Initial array - We are using the shell's original sequence
(N/2, N/4, ...1) as intervals in our algorithm.
In the first loop, if the array size isN = 8then, the elements lying at the interval ofN/2 = 4are compared and swapped if they are not in order.- The 0th element is compared with the 4th element.
- If the 0th element is greater than the 4th one then, the 4th element is first stored in
tempvariable and the0thelement (ie. greater element) is stored in the4thposition and the element stored intempis stored in the0thposition.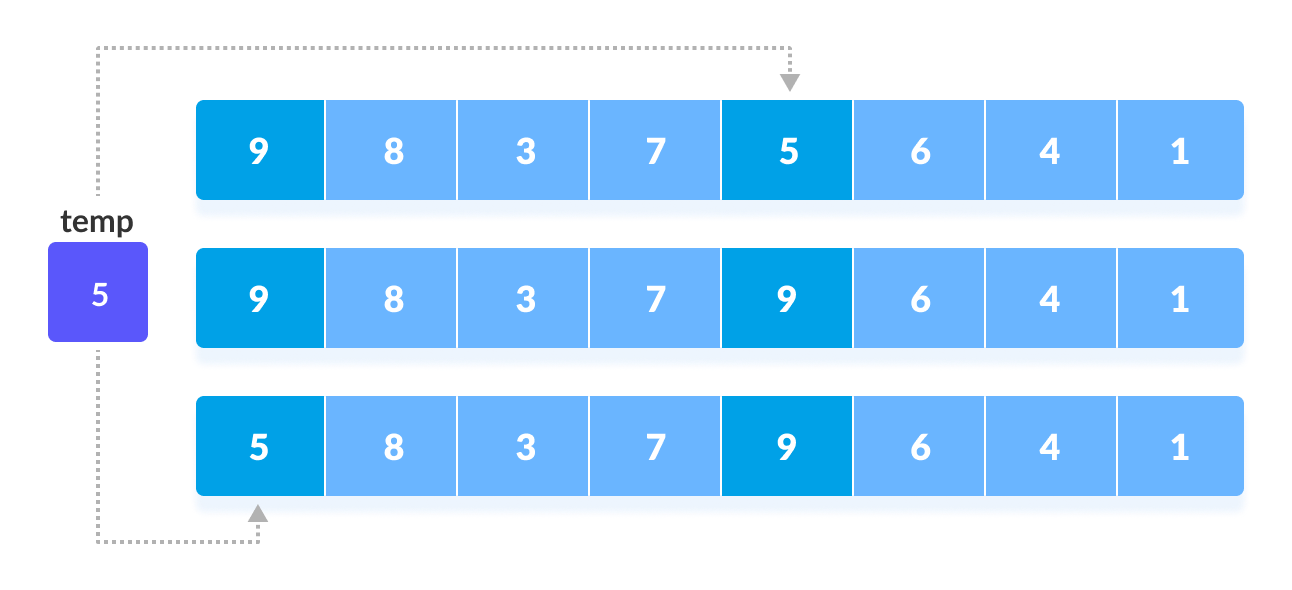
Rearrange the elements at n/2 interval
This process goes on for all the remaining elements.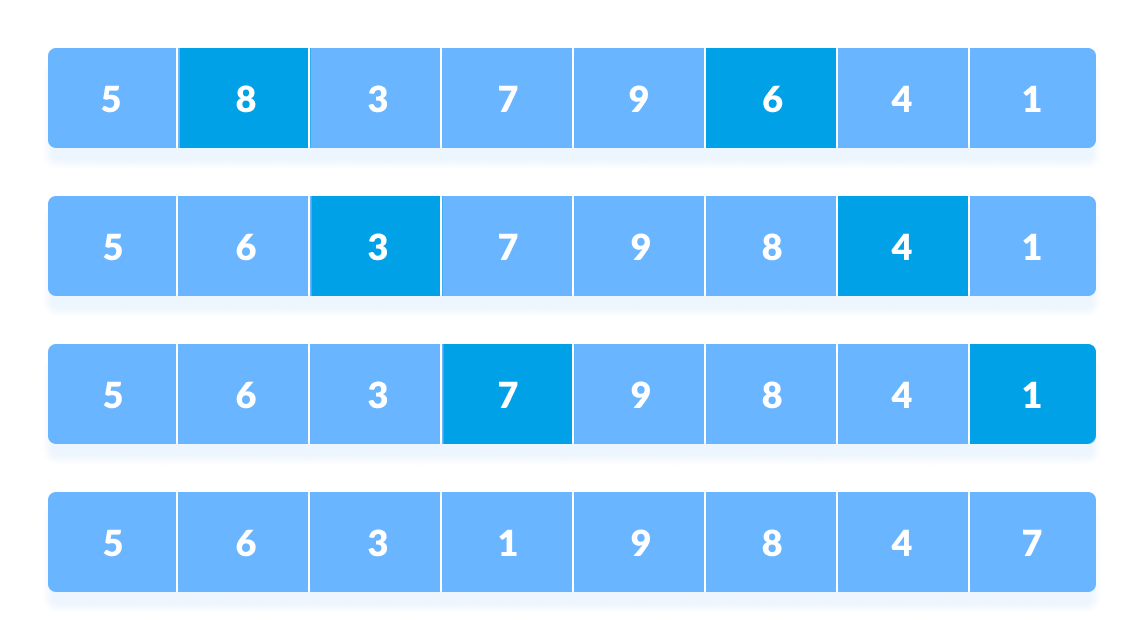
Rearrange all the elements at n/2 interval
- In the second loop, an interval of
N/4 = 8/4 = 2is taken and again the elements lying at these intervals are sorted.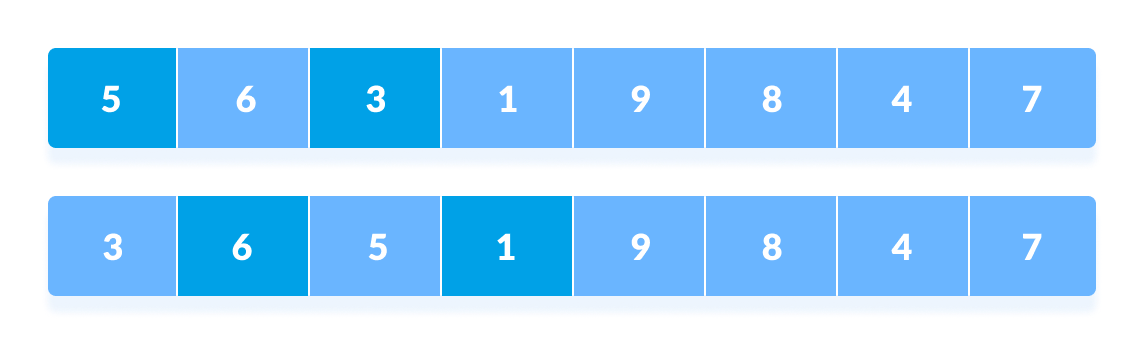
Rearrange the elements at n/4 interval
You might get confused at this point.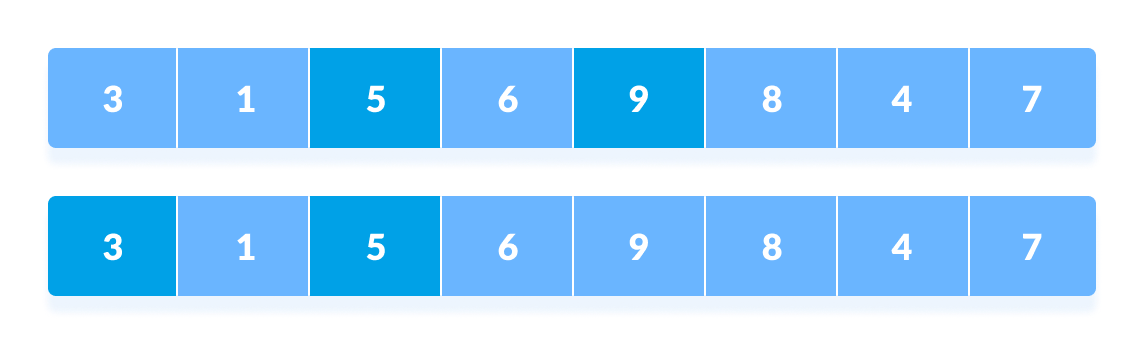
All the elements in the array lying at the current interval are compared.
The elements at 4th and2ndposition are compared. The elements at 2nd and0thposition are also compared. All the elements in the array lying at the current interval are compared. - The same process goes on for remaining elements.
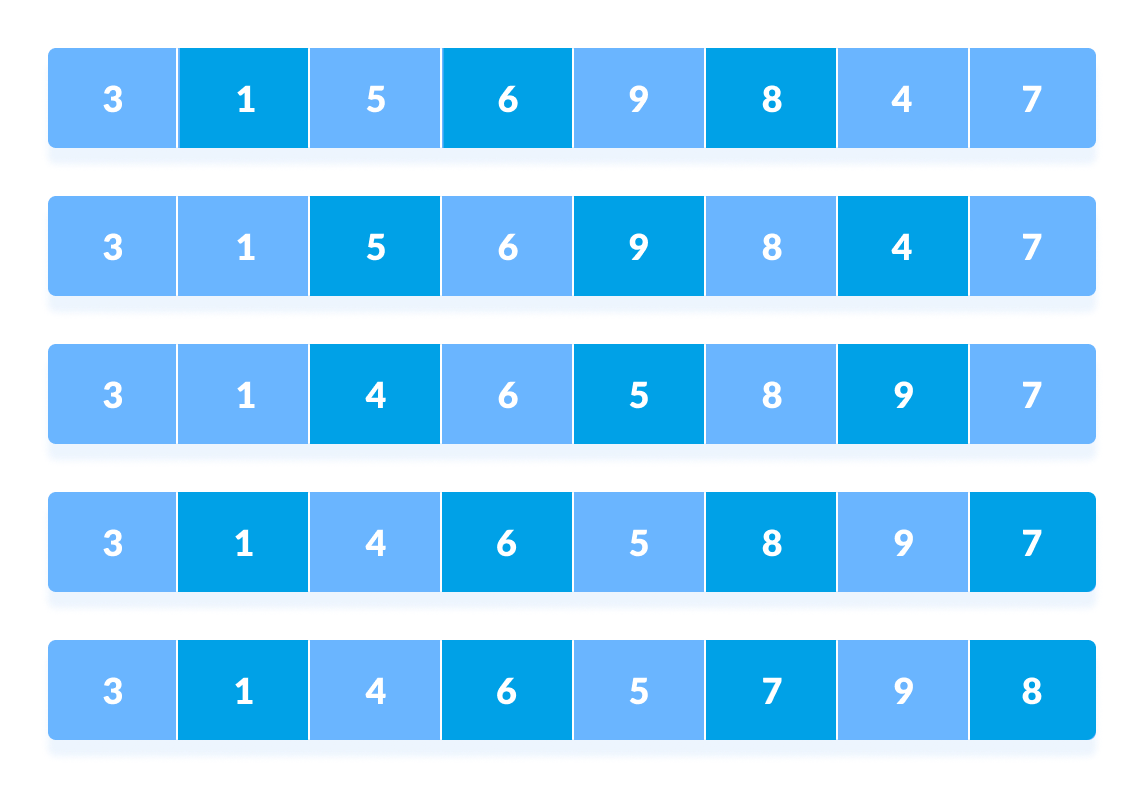
Rearrange all the elements at n/4 interval - Finally, when the interval is
N/8 = 8/8 =1then the array elements lying at the interval of 1 are sorted. The array is now completely sorted.
Rearrange the elements at n/8 interval
Shell Sort Algorithm
shellSort(array, size)
for interval i <- size/2n down to 1
for each interval "i" in array
sort all the elements at interval "i"
end shellSort
Shell Sort Code in Python, Java, and C/C++
# Shell sort in python
def shellSort(array, n):
# Rearrange elements at each n/2, n/4, n/8, ... intervals
interval = n // 2
while interval > 0:
for i in range(interval, n):
temp = array[i]
j = i
while j >= interval and array[j - interval] > temp:
array[j] = array[j - interval]
j -= interval
array[j] = temp
interval //= 2
data = [9, 8, 3, 7, 5, 6, 4, 1]
size = len(data)
shellSort(data, size)
print('Sorted Array in Ascending Order:')
print(data)
// Shell sort in Java programming
import java.util.Arrays;
// Shell sort
class ShellSort {
// Rearrange elements at each n/2, n/4, n/8, ... intervals
void shellSort(int array[], int n) {
for (int interval = n / 2; interval > 0; interval /= 2) {
for (int i = interval; i < n; i += 1) {
int temp = array[i];
int j;
for (j = i; j >= interval && array[j - interval] > temp; j -= interval) {
array[j] = array[j - interval];
}
array[j] = temp;
}
}
}
// Driver code
public static void main(String args[]) {
int[] data = { 9, 8, 3, 7, 5, 6, 4, 1 };
int size = data.length;
ShellSort ss = new ShellSort();
ss.shellSort(data, size);
System.out.println("Sorted Array in Ascending Order: ");
System.out.println(Arrays.toString(data));
}
}
// Shell Sort in C programming
#include <stdio.h>
// Shell sort
void shellSort(int array[], int n) {
// Rearrange elements at each n/2, n/4, n/8, ... intervals
for (int interval = n / 2; interval > 0; interval /= 2) {
for (int i = interval; i < n; i += 1) {
int temp = array[i];
int j;
for (j = i; j >= interval && array[j - interval] > temp; j -= interval) {
array[j] = array[j - interval];
}
array[j] = temp;
}
}
}
// Print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
printf("%d ", array[i]);
}
printf("\n");
}
// Driver code
int main() {
int data[] = {9, 8, 3, 7, 5, 6, 4, 1};
int size = sizeof(data) / sizeof(data[0]);
shellSort(data, size);
printf("Sorted array: \n");
printArray(data, size);
}
// Shell Sort in C++ programming
#include <iostream>
using namespace std;
// Shell sort
void shellSort(int array[], int n) {
// Rearrange elements at each n/2, n/4, n/8, ... intervals
for (int interval = n / 2; interval > 0; interval /= 2) {
for (int i = interval; i < n; i += 1) {
int temp = array[i];
int j;
for (j = i; j >= interval && array[j - interval] > temp; j -= interval) {
array[j] = array[j - interval];
}
array[j] = temp;
}
}
}
// Print an array
void printArray(int array[], int size) {
int i;
for (i = 0; i < size; i++)
cout << array[i] << " ";
cout << endl;
}
// Driver code
int main() {
int data[] = {9, 8, 3, 7, 5, 6, 4, 1};
int size = sizeof(data) / sizeof(data[0]);
shellSort(data, size);
cout << "Sorted array: \n";
printArray(data, size);
}
Shell Sort Complexity
| Time Complexity | |
|---|---|
| Best | O(nlog n) |
| Worst | O(n2) |
| Average | O(nlog n) |
| Space Complexity | O(1) |
| Stability | No |
Shell sort is an unstable sorting algorithm because this algorithm does not examine the elements lying in between the intervals.
Time Complexity
- Worst Case Complexity: less than or equal to
O(n2)
Worst case complexity for shell sort is always less than or equal toO(n2).
According to Poonen Theorem, worst case complexity for shell sort isΘ(Nlog N)2/(log log N)2)orΘ(Nlog N)2/log log N)orΘ(N(log N)2)or something in between. - Best Case Complexity:
O(n*log n)
When the array is already sorted, the total number of comparisons for each interval (or increment) is equal to the size of the array. - Average Case Complexity:
O(n*log n)
It is aroundO(n1.25).
The complexity depends on the interval chosen. The above complexities differ for different increment sequences chosen. Best increment sequence is unknown.
Space Complexity:
The space complexity for shell sort is O(1).
Shell Sort Applications
Shell sort is used when:
- calling a stack is overhead.
uClibclibrary uses this sort. - recursion exceeds a limit.
bzip2compressor uses it. - Insertion sort does not perform well when the close elements are far apart. Shell sort helps in reducing the distance between the close elements. Thus, there will be less number of swappings to be performed.
