Kruskal's algorithm is a minimum spanning tree algorithm that takes a graph as input and finds the subset of the edges of that graph which
- form a tree that includes every vertex
- has the minimum sum of weights among all the trees that can be formed from the graph
How Kruskal's algorithm works
It falls under a class of algorithms called greedy algorithms that find the local optimum in the hopes of finding a global optimum.
We start from the edges with the lowest weight and keep adding edges until we reach our goal.
The steps for implementing Kruskal's algorithm are as follows:
- Sort all the edges from low weight to high
- Take the edge with the lowest weight and add it to the spanning tree. If adding the edge created a cycle, then reject this edge.
- Keep adding edges until we reach all vertices.
Example of Kruskal's algorithm
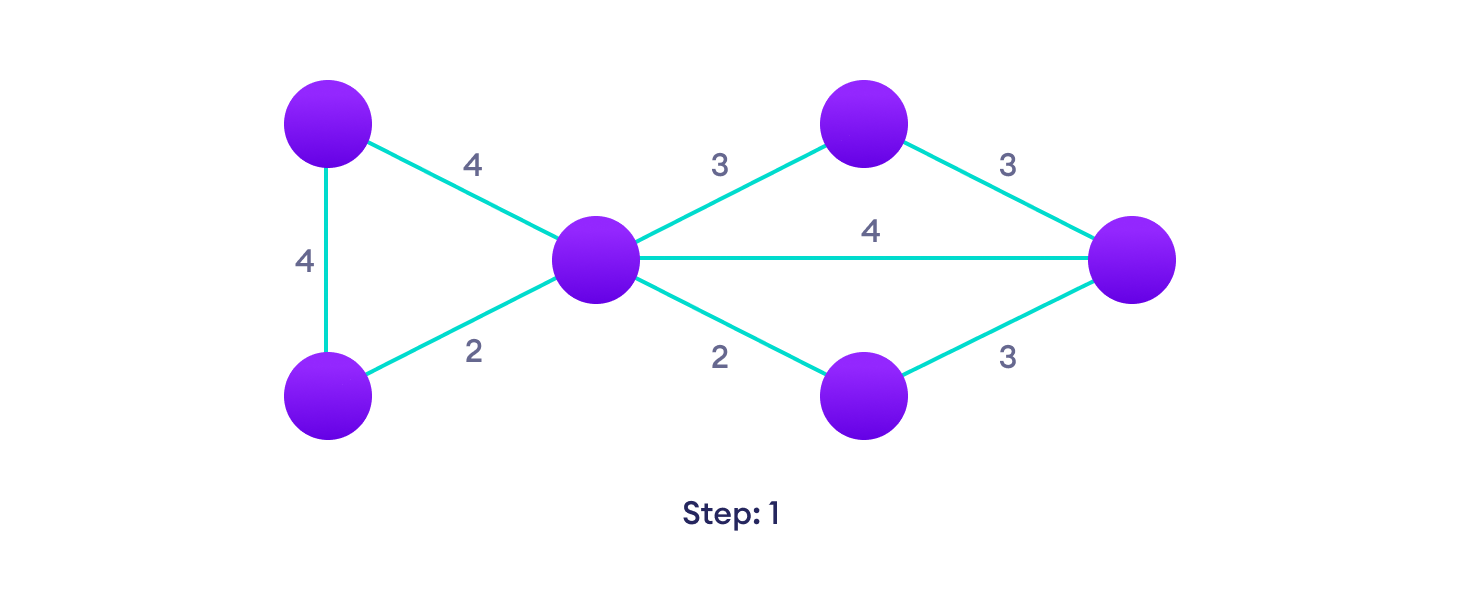
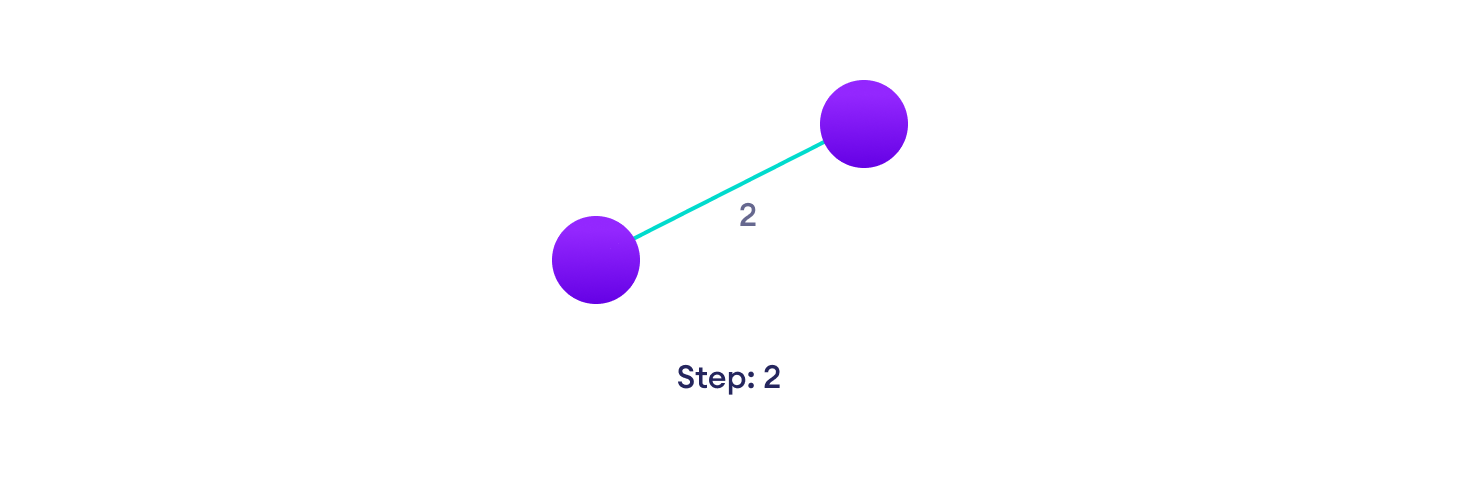
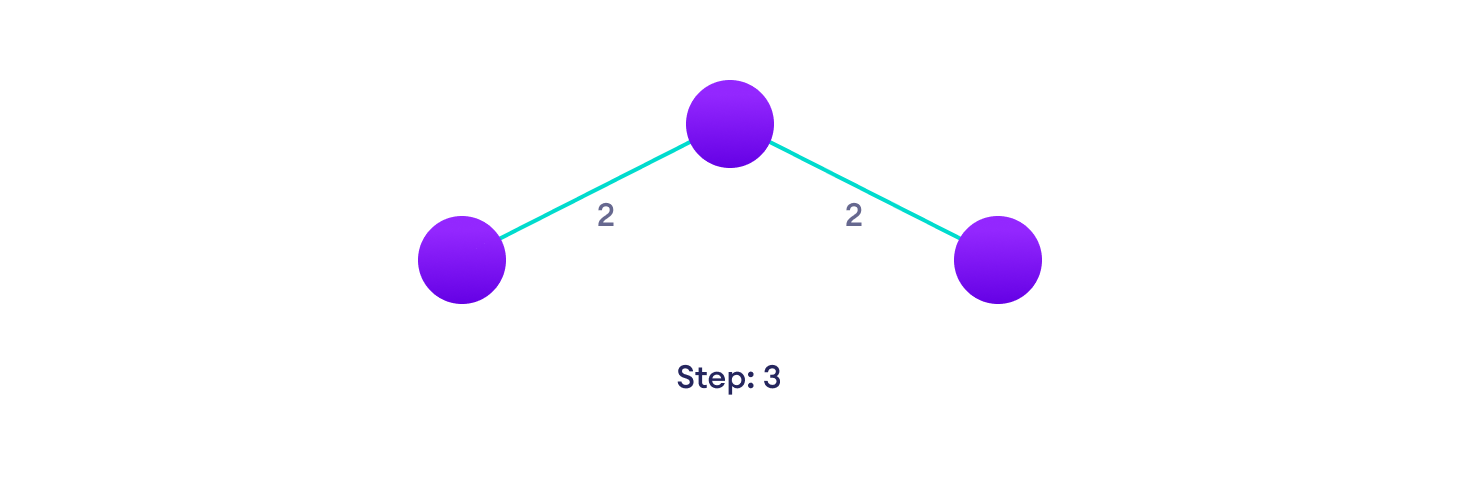
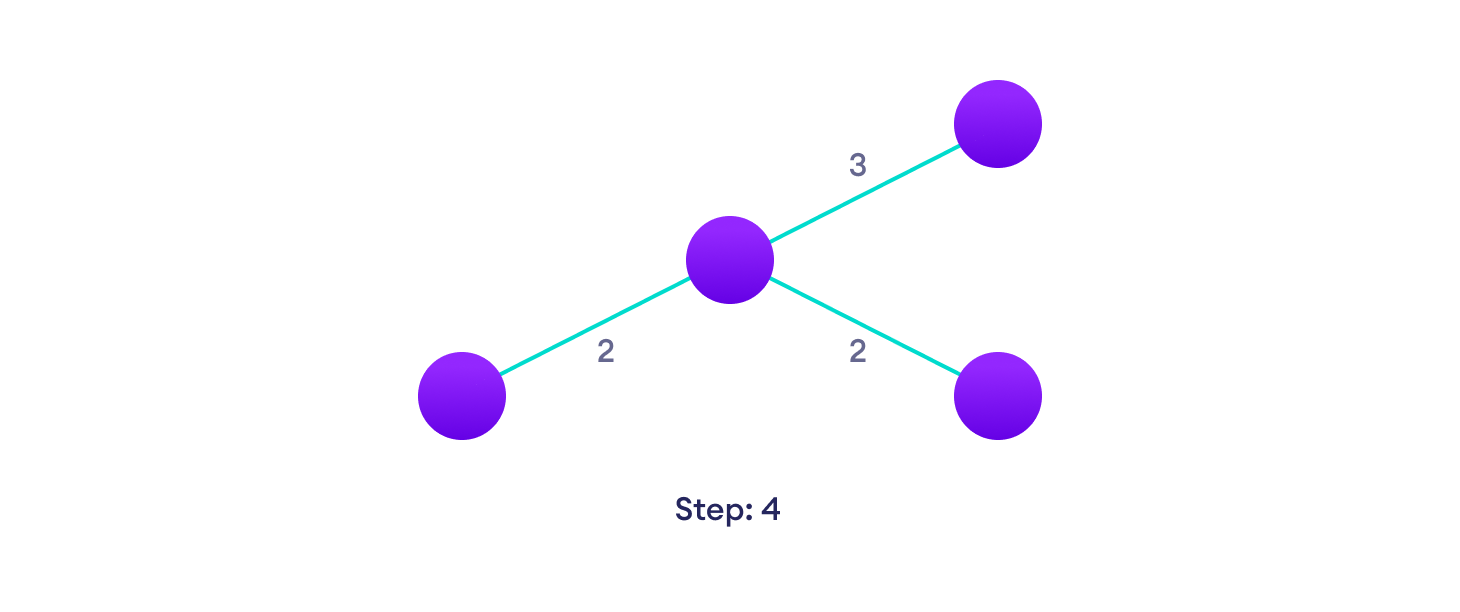
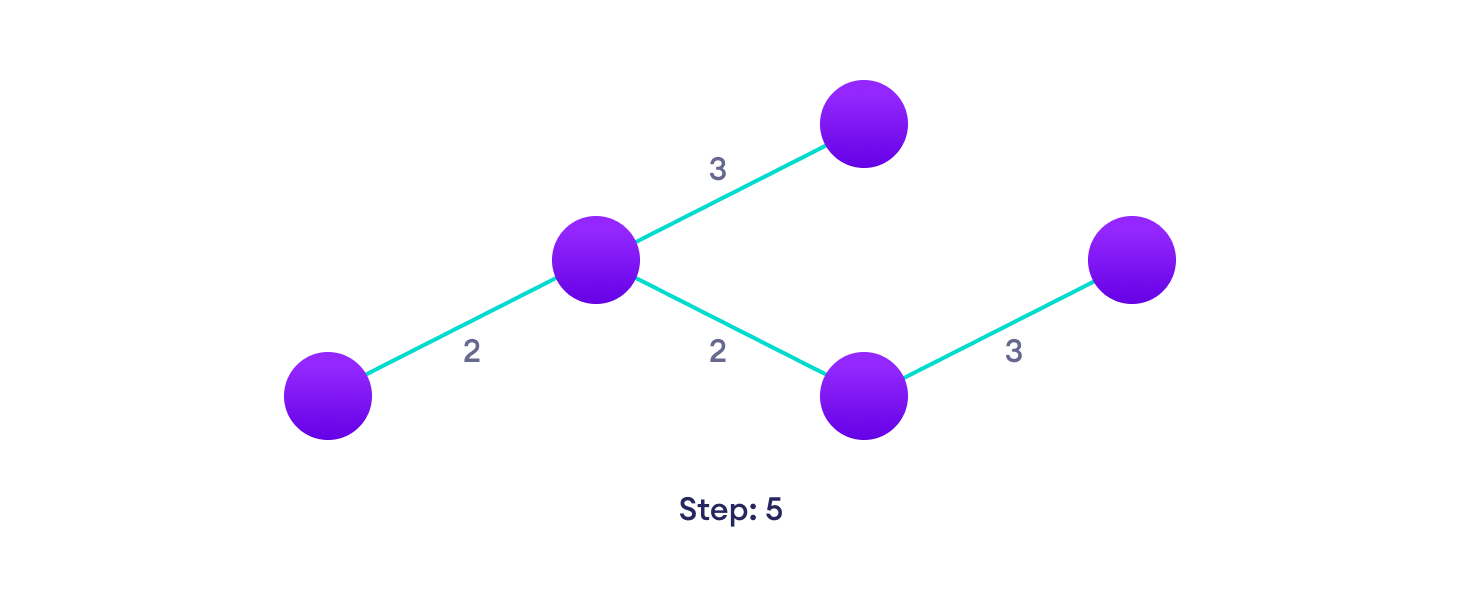
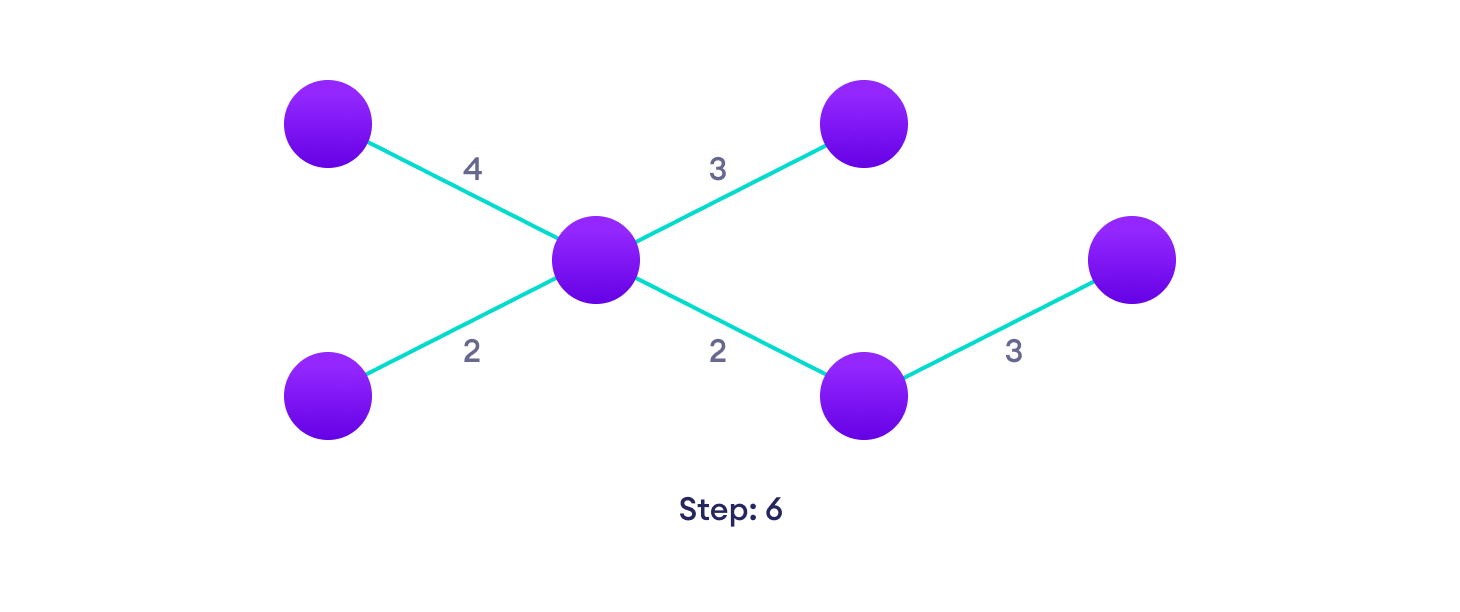
Kruskal Algorithm Pseudocode
Any minimum spanning tree algorithm revolves around checking if adding an edge creates a loop or not.
The most common way to find this out is an algorithm called Union FInd. The Union-Find algorithm divides the vertices into clusters and allows us to check if two vertices belong to the same cluster or not and hence decide whether adding an edge creates a cycle.
KRUSKAL(G):
A = ∅
For each vertex v ∈ G.V:
MAKE-SET(v)
For each edge (u, v) ∈ G.E ordered by increasing order by weight(u, v):
if FIND-SET(u) ≠ FIND-SET(v):
A = A ∪ {(u, v)}
UNION(u, v)
return A
Python, Java and C/C++ Examples
# Kruskal's algorithm in Python
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = []
def add_edge(self, u, v, w):
self.graph.append([u, v, w])
# Search function
def find(self, parent, i):
if parent[i] == i:
return i
return self.find(parent, parent[i])
def apply_union(self, parent, rank, x, y):
xroot = self.find(parent, x)
yroot = self.find(parent, y)
if rank[xroot] < rank[yroot]:
parent[xroot] = yroot
elif rank[xroot] > rank[yroot]:
parent[yroot] = xroot
else:
parent[yroot] = xroot
rank[xroot] += 1
# Applying Kruskal algorithm
def kruskal_algo(self):
result = []
i, e = 0, 0
self.graph = sorted(self.graph, key=lambda item: item[2])
parent = []
rank = []
for node in range(self.V):
parent.append(node)
rank.append(0)
while e < self.V - 1:
u, v, w = self.graph[i]
i = i + 1
x = self.find(parent, u)
y = self.find(parent, v)
if x != y:
e = e + 1
result.append([u, v, w])
self.apply_union(parent, rank, x, y)
for u, v, weight in result:
print("%d - %d: %d" % (u, v, weight))
g = Graph(6)
g.add_edge(0, 1, 4)
g.add_edge(0, 2, 4)
g.add_edge(1, 2, 2)
g.add_edge(1, 0, 4)
g.add_edge(2, 0, 4)
g.add_edge(2, 1, 2)
g.add_edge(2, 3, 3)
g.add_edge(2, 5, 2)
g.add_edge(2, 4, 4)
g.add_edge(3, 2, 3)
g.add_edge(3, 4, 3)
g.add_edge(4, 2, 4)
g.add_edge(4, 3, 3)
g.add_edge(5, 2, 2)
g.add_edge(5, 4, 3)
g.kruskal_algo()
// Kruskal's algorithm in Java
import java.util.*;
class Graph {
class Edge implements Comparable<Edge> {
int src, dest, weight;
public int compareTo(Edge compareEdge) {
return this.weight - compareEdge.weight;
}
};
// Union
class subset {
int parent, rank;
};
int vertices, edges;
Edge edge[];
// Graph creation
Graph(int v, int e) {
vertices = v;
edges = e;
edge = new Edge[edges];
for (int i = 0; i < e; ++i)
edge[i] = new Edge();
}
int find(subset subsets[], int i) {
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
void Union(subset subsets[], int x, int y) {
int xroot = find(subsets, x);
int yroot = find(subsets, y);
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Applying Krushkal Algorithm
void KruskalAlgo() {
Edge result[] = new Edge[vertices];
int e = 0;
int i = 0;
for (i = 0; i < vertices; ++i)
result[i] = new Edge();
// Sorting the edges
Arrays.sort(edge);
subset subsets[] = new subset[vertices];
for (i = 0; i < vertices; ++i)
subsets[i] = new subset();
for (int v = 0; v < vertices; ++v) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
i = 0;
while (e < vertices - 1) {
Edge next_edge = new Edge();
next_edge = edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
if (x != y) {
result[e++] = next_edge;
Union(subsets, x, y);
}
}
for (i = 0; i < e; ++i)
System.out.println(result[i].src + " - " + result[i].dest + ": " + result[i].weight);
}
public static void main(String[] args) {
int vertices = 6; // Number of vertices
int edges = 8; // Number of edges
Graph G = new Graph(vertices, edges);
G.edge[0].src = 0;
G.edge[0].dest = 1;
G.edge[0].weight = 4;
G.edge[1].src = 0;
G.edge[1].dest = 2;
G.edge[1].weight = 4;
G.edge[2].src = 1;
G.edge[2].dest = 2;
G.edge[2].weight = 2;
G.edge[3].src = 2;
G.edge[3].dest = 3;
G.edge[3].weight = 3;
G.edge[4].src = 2;
G.edge[4].dest = 5;
G.edge[4].weight = 2;
G.edge[5].src = 2;
G.edge[5].dest = 4;
G.edge[5].weight = 4;
G.edge[6].src = 3;
G.edge[6].dest = 4;
G.edge[6].weight = 3;
G.edge[7].src = 5;
G.edge[7].dest = 4;
G.edge[7].weight = 3;
G.KruskalAlgo();
}
}
// Kruskal's algorithm in C
#include <stdio.h>
#define MAX 30
typedef struct edge {
int u, v, w;
} edge;
typedef struct edge_list {
edge data[MAX];
int n;
} edge_list;
edge_list elist;
int Graph[MAX][MAX], n;
edge_list spanlist;
void kruskalAlgo();
int find(int belongs[], int vertexno);
void applyUnion(int belongs[], int c1, int c2);
void sort();
void print();
// Applying Krushkal Algo
void kruskalAlgo() {
int belongs[MAX], i, j, cno1, cno2;
elist.n = 0;
for (i = 1; i < n; i++)
for (j = 0; j < i; j++) {
if (Graph[i][j] != 0) {
elist.data[elist.n].u = i;
elist.data[elist.n].v = j;
elist.data[elist.n].w = Graph[i][j];
elist.n++;
}
}
sort();
for (i = 0; i < n; i++)
belongs[i] = i;
spanlist.n = 0;
for (i = 0; i < elist.n; i++) {
cno1 = find(belongs, elist.data[i].u);
cno2 = find(belongs, elist.data[i].v);
if (cno1 != cno2) {
spanlist.data[spanlist.n] = elist.data[i];
spanlist.n = spanlist.n + 1;
applyUnion(belongs, cno1, cno2);
}
}
}
int find(int belongs[], int vertexno) {
return (belongs[vertexno]);
}
void applyUnion(int belongs[], int c1, int c2) {
int i;
for (i = 0; i < n; i++)
if (belongs[i] == c2)
belongs[i] = c1;
}
// Sorting algo
void sort() {
int i, j;
edge temp;
for (i = 1; i < elist.n; i++)
for (j = 0; j < elist.n - 1; j++)
if (elist.data[j].w > elist.data[j + 1].w) {
temp = elist.data[j];
elist.data[j] = elist.data[j + 1];
elist.data[j + 1] = temp;
}
}
// Printing the result
void print() {
int i, cost = 0;
for (i = 0; i < spanlist.n; i++) {
printf("\n%d - %d : %d", spanlist.data[i].u, spanlist.data[i].v, spanlist.data[i].w);
cost = cost + spanlist.data[i].w;
}
printf("\nSpanning tree cost: %d", cost);
}
int main() {
int i, j, total_cost;
n = 6;
Graph[0][0] = 0;
Graph[0][1] = 4;
Graph[0][2] = 4;
Graph[0][3] = 0;
Graph[0][4] = 0;
Graph[0][5] = 0;
Graph[0][6] = 0;
Graph[1][0] = 4;
Graph[1][1] = 0;
Graph[1][2] = 2;
Graph[1][3] = 0;
Graph[1][4] = 0;
Graph[1][5] = 0;
Graph[1][6] = 0;
Graph[2][0] = 4;
Graph[2][1] = 2;
Graph[2][2] = 0;
Graph[2][3] = 3;
Graph[2][4] = 4;
Graph[2][5] = 0;
Graph[2][6] = 0;
Graph[3][0] = 0;
Graph[3][1] = 0;
Graph[3][2] = 3;
Graph[3][3] = 0;
Graph[3][4] = 3;
Graph[3][5] = 0;
Graph[3][6] = 0;
Graph[4][0] = 0;
Graph[4][1] = 0;
Graph[4][2] = 4;
Graph[4][3] = 3;
Graph[4][4] = 0;
Graph[4][5] = 0;
Graph[4][6] = 0;
Graph[5][0] = 0;
Graph[5][1] = 0;
Graph[5][2] = 2;
Graph[5][3] = 0;
Graph[5][4] = 3;
Graph[5][5] = 0;
Graph[5][6] = 0;
kruskalAlgo();
print();
}
// Kruskal's algorithm in C++
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
#define edge pair<int, int>
class Graph {
private:
vector<pair<int, edge> > G; // graph
vector<pair<int, edge> > T; // mst
int *parent;
int V; // number of vertices/nodes in graph
public:
Graph(int V);
void AddWeightedEdge(int u, int v, int w);
int find_set(int i);
void union_set(int u, int v);
void kruskal();
void print();
};
Graph::Graph(int V) {
parent = new int[V];
//i 0 1 2 3 4 5
//parent[i] 0 1 2 3 4 5
for (int i = 0; i < V; i++)
parent[i] = i;
G.clear();
T.clear();
}
void Graph::AddWeightedEdge(int u, int v, int w) {
G.push_back(make_pair(w, edge(u, v)));
}
int Graph::find_set(int i) {
// If i is the parent of itself
if (i == parent[i])
return i;
else
// Else if i is not the parent of itself
// Then i is not the representative of his set,
// so we recursively call Find on its parent
return find_set(parent[i]);
}
void Graph::union_set(int u, int v) {
parent[u] = parent[v];
}
void Graph::kruskal() {
int i, uRep, vRep;
sort(G.begin(), G.end()); // increasing weight
for (i = 0; i < G.size(); i++) {
uRep = find_set(G[i].second.first);
vRep = find_set(G[i].second.second);
if (uRep != vRep) {
T.push_back(G[i]); // add to tree
union_set(uRep, vRep);
}
}
}
void Graph::print() {
cout << "Edge :"
<< " Weight" << endl;
for (int i = 0; i < T.size(); i++) {
cout << T[i].second.first << " - " << T[i].second.second << " : "
<< T[i].first;
cout << endl;
}
}
int main() {
Graph g(6);
g.AddWeightedEdge(0, 1, 4);
g.AddWeightedEdge(0, 2, 4);
g.AddWeightedEdge(1, 2, 2);
g.AddWeightedEdge(1, 0, 4);
g.AddWeightedEdge(2, 0, 4);
g.AddWeightedEdge(2, 1, 2);
g.AddWeightedEdge(2, 3, 3);
g.AddWeightedEdge(2, 5, 2);
g.AddWeightedEdge(2, 4, 4);
g.AddWeightedEdge(3, 2, 3);
g.AddWeightedEdge(3, 4, 3);
g.AddWeightedEdge(4, 2, 4);
g.AddWeightedEdge(4, 3, 3);
g.AddWeightedEdge(5, 2, 2);
g.AddWeightedEdge(5, 4, 3);
g.kruskal();
g.print();
return 0;
}
Kruskal's vs Prim's Algorithm
Prim's algorithm is another popular minimum spanning tree algorithm that uses a different logic to find the MST of a graph. Instead of starting from an edge, Prim's algorithm starts from a vertex and keeps adding lowest-weight edges which aren't in the tree, until all vertices have been covered.
Kruskal's Algorithm Complexity
The time complexity Of Kruskal's Algorithm is: O(E log E).
Kruskal's Algorithm Applications
- In order to layout electrical wiring
- In computer network (LAN connection)
