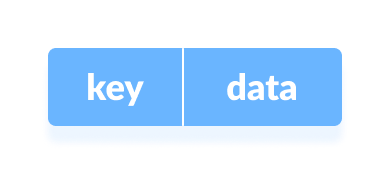
The Hash table data structure stores elements in key-value pairs where
- Key- unique integer that is used for indexing the values
- Value - data that are associated with keys.
Hashing (Hash Function)
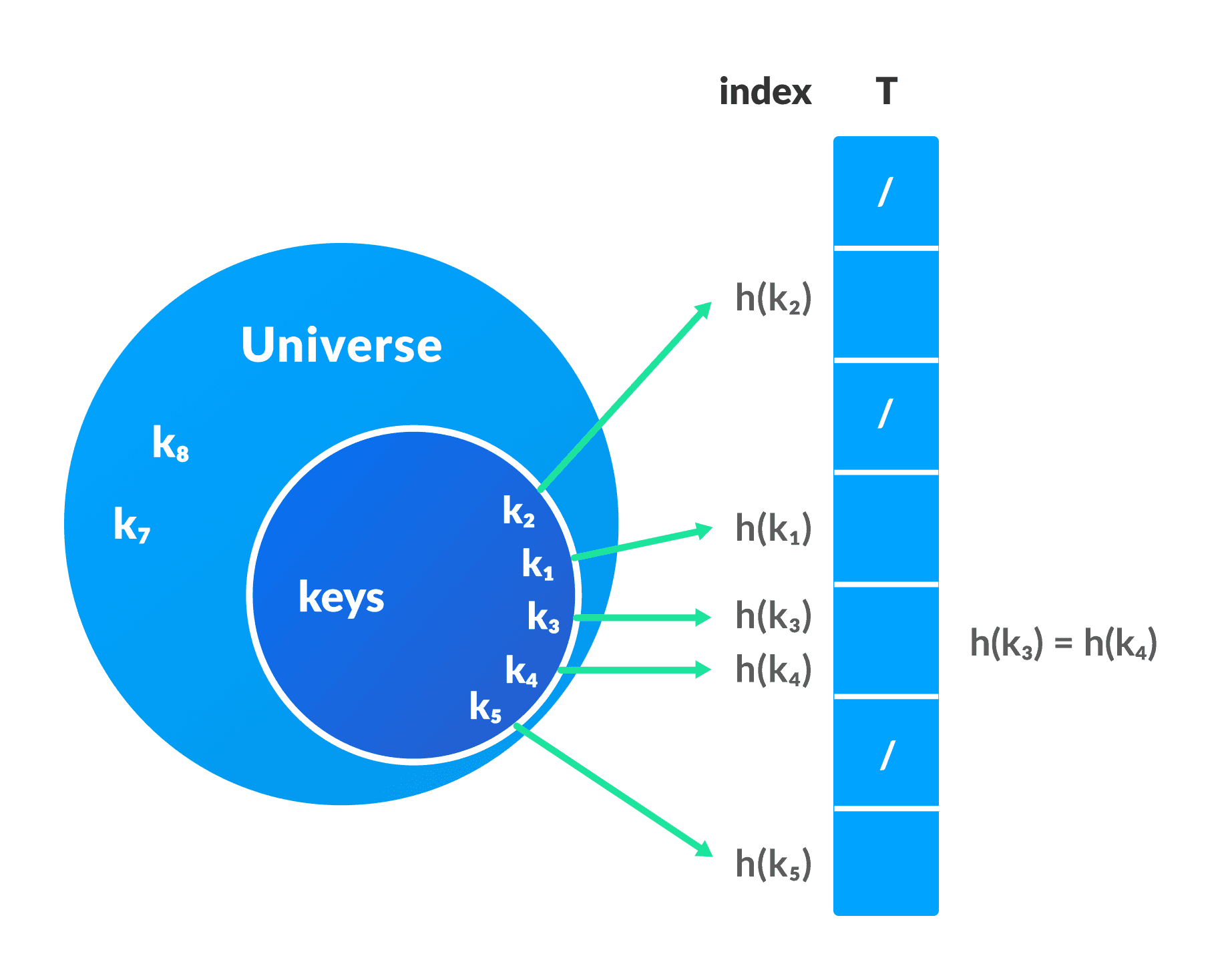
In a hash table, a new index is processed using the keys. And, the element corresponding to that key is stored in the index. This process is called hashing.
Let k be a key and h(x) be a hash function.
Here, h(k) will give us a new index to store the element linked with k.
To learn more, visit Hashing.
Hash Collision
When the hash function generates the same index for multiple keys, there will be a conflict (what value to be stored in that index). This is called a hash collision.
We can resolve the hash collision using one of the following techniques.
- Collision resolution by chaining
- Open Addressing: Linear/Quadratic Probing and Double Hashing
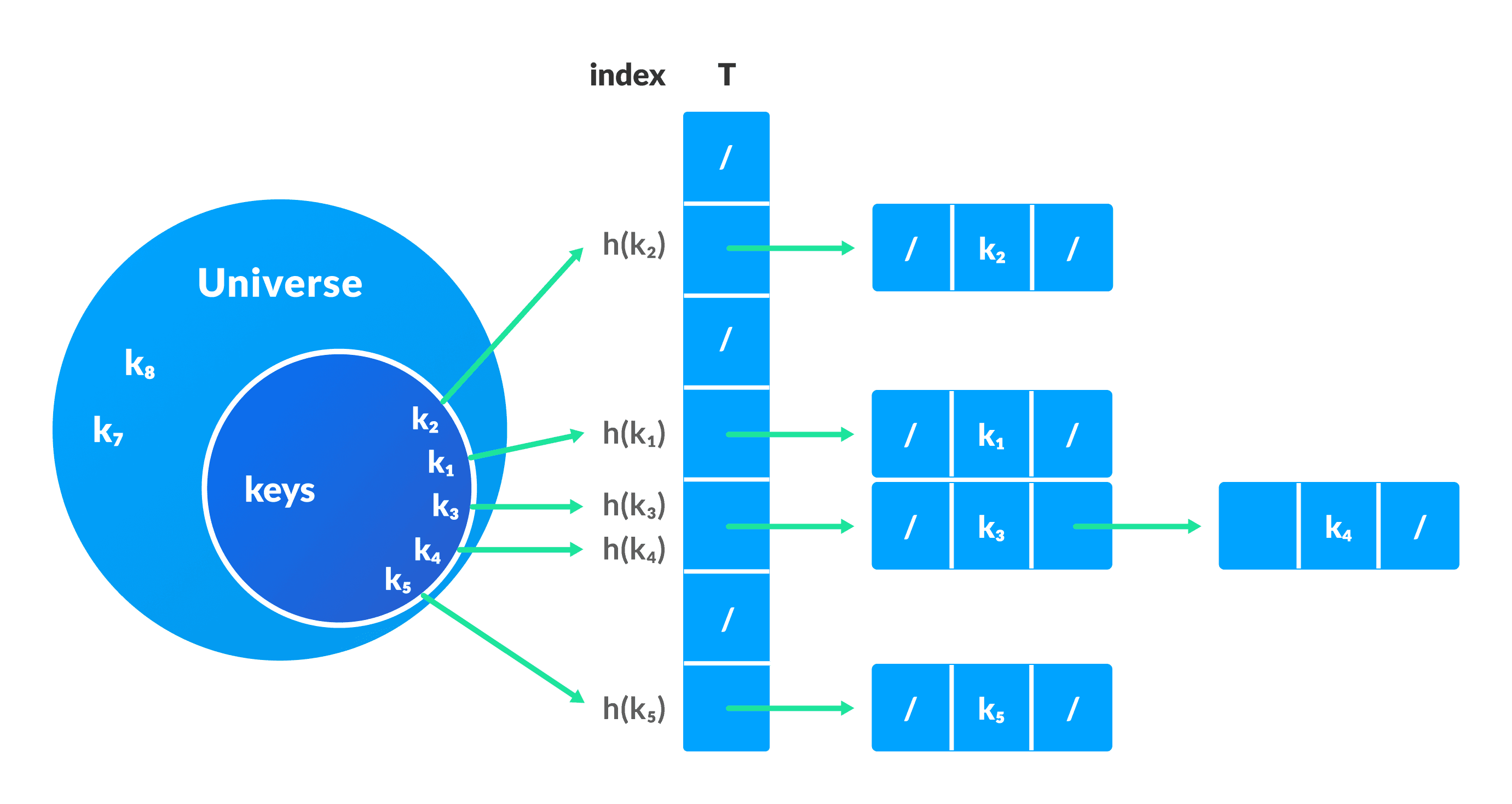
1. Collision resolution by chaining
In chaining, if a hash function produces the same index for multiple elements, these elements are stored in the same index by using a doubly-linked list.
If j is the slot for multiple elements, it contains a pointer to the head of the list of elements. If no element is present, j contains NIL.
Pseudocode for operations
chainedHashSearch(T, k)
return T[h(k)]
chainedHashInsert(T, x)
T[h(x.key)] = x //insert at the head
chainedHashDelete(T, x)
T[h(x.key)] = NIL
2. Open Addressing
Unlike chaining, open addressing doesn't store multiple elements into the same slot. Here, each slot is either filled with a single key or left NIL.
Different techniques used in open addressing are:
i. Linear Probing
In linear probing, collision is resolved by checking the next slot.
h(k, i) = (h′(k) + i) mod m
where
i = {0, 1, ….}h'(k)is a new hash function
If a collision occurs at h(k, 0), then h(k, 1) is checked. In this way, the value of i is incremented linearly.
The problem with linear probing is that a cluster of adjacent slots is filled. When inserting a new element, the entire cluster must be traversed. This adds to the time required to perform operations on the hash table.
ii. Quadratic Probing
It works similar to linear probing but the spacing between the slots is increased (greater than one) by using the following relation.
h(k, i) = (h′(k) + c1i + c2i2) mod m
where,
c1andc2are positive auxiliary constants,i = {0, 1, ….}
iii. Double hashing
If a collision occurs after applying a hash function h(k), then another hash function is calculated for finding the next slot.
h(k, i) = (h1(k) + ih2(k)) mod m
Good Hash Functions
A good hash function may not prevent the collisions completely however it can reduce the number of collisions.
Here, we will look into different methods to find a good hash function
1. Division Method
If k is a key and m is the size of the hash table, the hash function h() is calculated as:
h(k) = k mod m
For example, If the size of a hash table is 10 and k = 112 then h(k) = 112 mod 10 = 2. The value of m must not be the powers of 2. This is because the powers of 2 in binary format are 10, 100, 1000, …. When we find k mod m, we will always get the lower order p-bits.
if m = 22, k = 17, then h(k) = 17 mod 22 = 10001 mod 100 = 01 if m = 23, k = 17, then h(k) = 17 mod 22 = 10001 mod 100 = 001 if m = 24, k = 17, then h(k) = 17 mod 22 = 10001 mod 100 = 0001 if m = 2p, then h(k) = p lower bits of m
2. Multiplication Method
h(k) = ⌊m(kA mod 1)⌋
where,
kA mod 1gives the fractional partkA,⌊ ⌋gives the floor valueAis any constant. The value ofAlies between 0 and 1. But, an optimal choice will be≈ (√5-1)/2suggested by Knuth.
3. Universal Hashing
In Universal hashing, the hash function is chosen at random independent of keys.
Python, Java and C/C++ Examples
# Python program to demonstrate working of HashTable
# Initialize the hash table with 10 empty lists (each index is a list to handle collisions)
hashTable = [[] for _ in range(10)]
def checkPrime(n):
if n == 1 or n == 0:
return 0
for i in range(2, n // 2):
if n % i == 0:
return 0
return 1
def getPrime(n):
if n % 2 == 0:
n = n + 1
while not checkPrime(n):
n += 2
return n
def hashFunction(key):
capacity = getPrime(10)
return key % capacity
def insertData(key, data):
index = hashFunction(key)
# Check if the key already exists in the list to update it, otherwise append
found = False
for i, kv in enumerate(hashTable[index]):
if kv[0] == key:
hashTable[index][i] = (key, data) # Update existing key-value pair
found = True
break
if not found:
hashTable[index].append((key, data)) # Add new key-value pair if not found
def removeData(key):
index = hashFunction(key)
# Remove the key-value pair from the list if it exists
for i, kv in enumerate(hashTable[index]):
if kv[0] == key:
del hashTable[index][i]
break
# Test the hash table
insertData(123, "apple")
insertData(432, "mango")
insertData(213, "banana")
insertData(654, "guava")
insertData(213, "orange") # This should update the value for key 213
print(hashTable)
removeData(123)
print(hashTable)
// Java program to demonstrate working of HashTable
import java.util.*;
class HashTable {
public static void main(String args[])
{
Hashtable<Integer, Integer>
ht = new Hashtable<Integer, Integer>();
ht.put(123, 432);
ht.put(12, 2345);
ht.put(15, 5643);
ht.put(3, 321);
ht.remove(12);
System.out.println(ht);
}
}
// Implementing hash table in C
#include <stdio.h>
#include <stdlib.h>
struct set
{
int key;
int data;
};
struct set *array;
int capacity = 10;
int size = 0;
int hashFunction(int key)
{
return (key % capacity);
}
int checkPrime(int n)
{
int i;
if (n == 1 || n == 0)
{
return 0;
}
for (i = 2; i < n / 2; i++)
{
if (n % i == 0)
{
return 0;
}
}
return 1;
}
int getPrime(int n)
{
if (n % 2 == 0)
{
n++;
}
while (!checkPrime(n))
{
n += 2;
}
return n;
}
void init_array()
{
capacity = getPrime(capacity);
array = (struct set *)malloc(capacity * sizeof(struct set));
for (int i = 0; i < capacity; i++)
{
array[i].key = 0;
array[i].data = 0;
}
}
void insert(int key, int data)
{
int index = hashFunction(key);
if (array[index].data == 0)
{
array[index].key = key;
array[index].data = data;
size++;
printf("\n Key (%d) has been inserted \n", key);
}
else if (array[index].key == key)
{
array[index].data = data;
}
else
{
printf("\n Collision occured \n");
}
}
void remove_element(int key)
{
int index = hashFunction(key);
if (array[index].data == 0)
{
printf("\n This key does not exist \n");
}
else
{
array[index].key = 0;
array[index].data = 0;
size--;
printf("\n Key (%d) has been removed \n", key);
}
}
void display()
{
int i;
for (i = 0; i < capacity; i++)
{
if (array[i].data == 0)
{
printf("\n array[%d]: / ", i);
}
else
{
printf("\n key: %d array[%d]: %d \t", array[i].key, i, array[i].data);
}
}
}
int size_of_hashtable()
{
return size;
}
int main()
{
int choice, key, data, n;
int c = 0;
init_array();
do
{
printf("1.Insert item in the Hash Table"
"\n2.Remove item from the Hash Table"
"\n3.Check the size of Hash Table"
"\n4.Display a Hash Table"
"\n\n Please enter your choice: ");
scanf("%d", &choice);
switch (choice)
{
case 1:
printf("Enter key -:\t");
scanf("%d", &key);
printf("Enter data -:\t");
scanf("%d", &data);
insert(key, data);
break;
case 2:
printf("Enter the key to delete-:");
scanf("%d", &key);
remove_element(key);
break;
case 3:
n = size_of_hashtable();
printf("Size of Hash Table is-:%d\n", n);
break;
case 4:
display();
break;
default:
printf("Invalid Input\n");
}
printf("\nDo you want to continue (press 1 for yes): ");
scanf("%d", &c);
} while (c == 1);
}
// Implementing hash table in C++
#include <iostream>
#include <list>
using namespace std;
class HashTable
{
int capacity;
list<int> *table;
public:
HashTable(int V);
void insertItem(int key, int data);
void deleteItem(int key);
int checkPrime(int n)
{
int i;
if (n == 1 || n == 0)
{
return 0;
}
for (i = 2; i < n / 2; i++)
{
if (n % i == 0)
{
return 0;
}
}
return 1;
}
int getPrime(int n)
{
if (n % 2 == 0)
{
n++;
}
while (!checkPrime(n))
{
n += 2;
}
return n;
}
int hashFunction(int key)
{
return (key % capacity);
}
void displayHash();
};
HashTable::HashTable(int c)
{
int size = getPrime(c);
this->capacity = size;
table = new list<int>[capacity];
}
void HashTable::insertItem(int key, int data)
{
int index = hashFunction(key);
table[index].push_back(data);
}
void HashTable::deleteItem(int key)
{
int index = hashFunction(key);
list<int>::iterator i;
for (i = table[index].begin();
i != table[index].end(); i++)
{
if (*i == key)
break;
}
if (i != table[index].end())
table[index].erase(i);
}
void HashTable::displayHash()
{
for (int i = 0; i < capacity; i++)
{
cout << "table[" << i << "]";
for (auto x : table[i])
cout << " --> " << x;
cout << endl;
}
}
int main()
{
int key[] = {231, 321, 212, 321, 433, 262};
int data[] = {123, 432, 523, 43, 423, 111};
int size = sizeof(key) / sizeof(key[0]);
HashTable h(size);
for (int i = 0; i < size; i++)
h.insertItem(key[i], data[i]);
h.deleteItem(12);
h.displayHash();
}
Applications of Hash Table
Hash tables are implemented where
- constant time lookup and insertion is required
- cryptographic applications
- indexing data is required
