A perfect binary tree is a type of binary tree in which every internal node has exactly two child nodes and all the leaf nodes are at the same level.
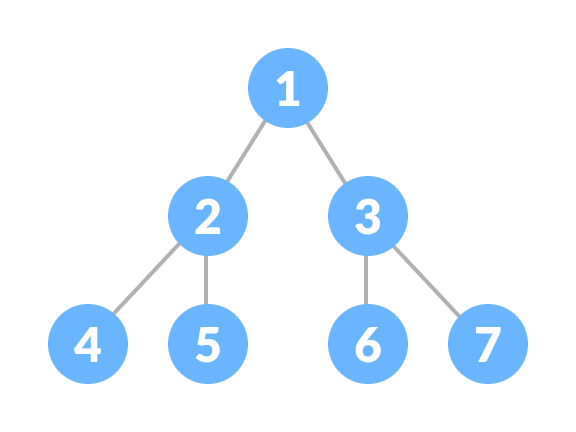
All the internal nodes have a degree of 2.
Recursively, a perfect binary tree can be defined as:
- If a single node has no children, it is a perfect binary tree of height
h = 0, - If a node has
h > 0, it is a perfect binary tree if both of its subtrees are of heighth - 1and are non-overlapping.
Python, Java and C/C++ Examples
The following code is for checking whether a tree is a perfect binary tree.
# Checking if a binary tree is a perfect binary tree in Python
class newNode:
def __init__(self, k):
self.key = k
self.right = self.left = None
# calculate the depth of the tree
def calculateDepth(node):
if node is None:
return 0
left_depth = calculateDepth(node.left)
right_depth = calculateDepth(node.right)
return max(left_depth, right_depth) + 1
# check if the tree is a perfect binary tree
def is_perfect(root, d, level=0):
# check if the tree is empty
if root is None:
return True
# check the presence of leaves
if root.left is None and root.right is None:
return d == level + 1
if root.left is None or root.right is None:
return False
return is_perfect(root.left, d, level + 1) and is_perfect(root.right, d, level + 1)
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)
root.right.left = newNode(6)
root.right.right = newNode(7)
if is_perfect(root, calculateDepth(root)):
print("The tree is a perfect binary tree")
else:
print("The tree is not a perfect binary tree")
// Checking if a binary tree is a perfect binary tree in Java
class PerfectBinaryTree {
static class Node {
int key;
Node left, right;
}
// calculate the depth of the tree considering both left and right subtrees
static int depth(Node node) {
if (node == null) {
return 0;
}
int leftDepth = depth(node.left);
int rightDepth = depth(node.right);
return Math.max(leftDepth, rightDepth) + 1;
}
// check if the tree is a perfect binary tree
static boolean is_perfect(Node root, int d, int level) {
// check if the tree is empty
if (root == null)
return true;
// check the presence of leaves
if (root.left == null && root.right == null)
return (d == level + 1);
if (root.left == null || root.right == null)
return false;
return is_perfect(root.left, d, level + 1) && is_perfect(root.right, d, level + 1);
}
// wrapper function
static boolean is_Perfect(Node root) {
int d = depth(root);
return is_perfect(root, d, 0);
}
// create a new node
static Node newNode(int k) {
Node node = new Node();
node.key = k;
node.right = null;
node.left = null;
return node;
}
public static void main(String args[]) {
Node root = null;
root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(6);
root.right.right = newNode(7);
if (is_Perfect(root))
System.out.println("The tree is a perfect binary tree");
else
System.out.println("The tree is not a perfect binary tree");
}
}
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node *left;
struct node *right;
};
// creating a new node
struct node *newnode(int data) {
struct node *node = (struct node *)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
// calculate the depth considering both left and right subtrees
int depth(struct node *node) {
if (node == NULL) {
return 0;
}
int leftDepth = depth(node->left);
int rightDepth = depth(node->right);
return (leftDepth > rightDepth ? leftDepth : rightDepth) + 1;
}
// check if the tree is perfect
bool is_perfect(struct node *root, int d, int level) {
// Check if the tree is empty
if (root == NULL)
return true;
// check the presence of children
if (root->left == NULL && root->right == NULL)
return (d == level + 1);
if (root->left == NULL || root->right == NULL)
return false;
return is_perfect(root->left, d, level + 1) &&
is_perfect(root->right, d, level + 1);
}
// wrapper function
bool is_Perfect(struct node *root) {
int d = depth(root);
return is_perfect(root, d, 0);
}
int main() {
struct node *root = NULL;
root = newnode(1);
root->left = newnode(2);
root->right = newnode(3);
root->left->left = newnode(4);
root->left->right = newnode(5);
root->right->left = newnode(6);
root->right->right = newnode(7);
if (is_Perfect(root))
printf("The tree is a perfect binary tree\n");
else
printf("The tree is not a perfect binary tree\n");
return 0;
}
// Checking if a binary tree is a perfect binary tree in C++
#include <iostream>
using namespace std;
struct Node {
int key;
struct Node *left, *right;
};
// calculate the depth considering both left and right subtrees
int depth(Node *node) {
if (node == NULL) {
return 0;
}
int leftDepth = depth(node->left);
int rightDepth = depth(node->right);
return max(leftDepth, rightDepth) + 1;
}
// check if the tree is a perfect binary tree
bool isPerfectR(struct Node *root, int d, int level = 0) {
if (root == NULL)
return true;
if (root->left == NULL && root->right == NULL)
return (d == level + 1);
if (root->left == NULL || root->right == NULL)
return false;
return isPerfectR(root->left, d, level + 1) &&
isPerfectR(root->right, d, level + 1);
}
bool isPerfect(Node *root) {
int d = depth(root);
return isPerfectR(root, d);
}
// create a new node
struct Node *newNode(int k) {
struct Node *node = new Node;
node->key = k;
node->right = node->left = NULL;
return node;
}
int main() {
struct Node *root = NULL;
root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
if (isPerfect(root))
cout << "The tree is a perfect binary tree\n";
else
cout << "The tree is not a perfect binary tree\n";
return 0;
}
Perfect Binary Tree Theorems
- A perfect binary tree of height h has
2h + 1– 1node. - A perfect binary tree with n nodes has height
log(n + 1) – 1 = Θ(ln(n)). - A perfect binary tree of height h has
2hleaf nodes. - The average depth of a node in a perfect binary tree is
Θ(ln(n)).
