An adjacency list represents a graph as an array of linked lists. The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.
For example, we have a graph below.
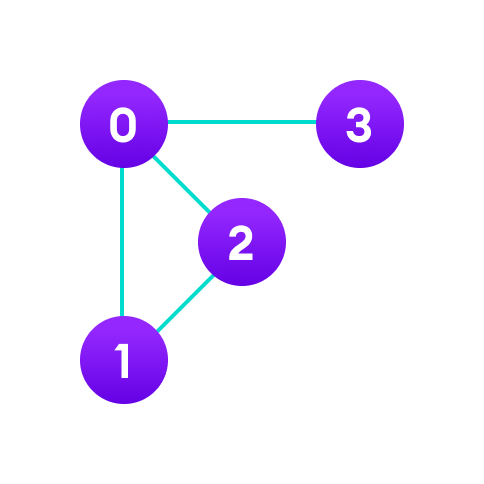
We can represent this graph in the form of a linked list on a computer as shown below.
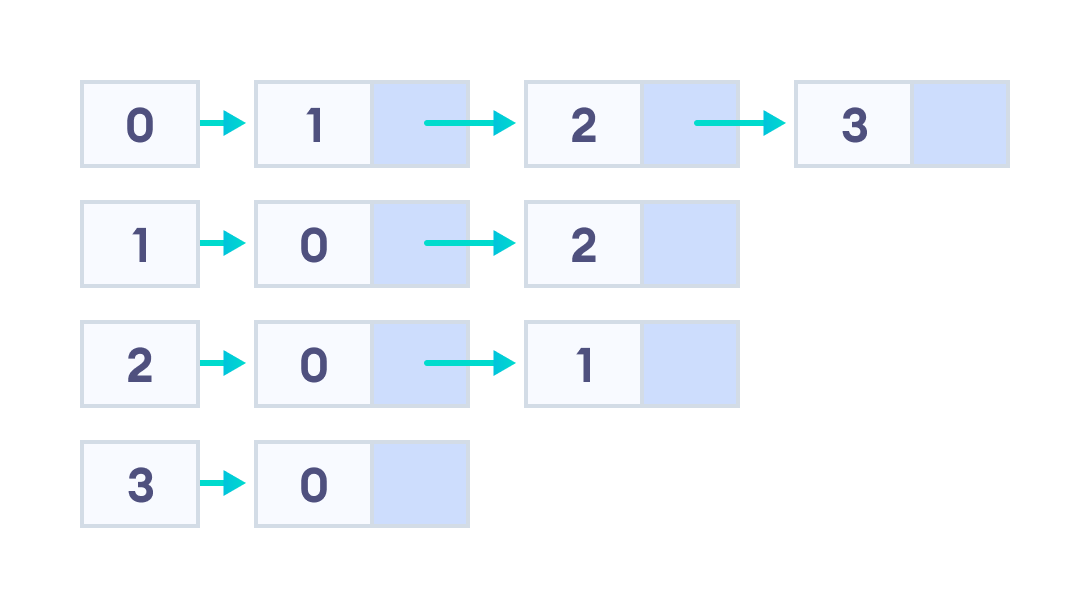
Here, 0, 1, 2, 3 are the vertices and each of them forms a linked list with all of its adjacent vertices. For instance, vertex 1 has two adjacent vertices 0 and 2. Therefore, 1 is linked with 0 and 2 in the figure above.
Pros of Adjacency List
- An adjacency list is efficient in terms of storage because we only need to store the values for the edges. For a sparse graph with millions of vertices and edges, this can mean a lot of saved space.
- It also helps to find all the vertices adjacent to a vertex easily.
Cons of Adjacency List
- Finding the adjacent list is not quicker than the adjacency matrix because all the connected nodes must be first explored to find them.
Adjacency List Structure
The simplest adjacency list needs a node data structure to store a vertex and a graph data structure to organize the nodes.
We stay close to the basic definition of a graph - a collection of vertices and edges {V, E}. For simplicity, we use an unlabeled graph as opposed to a labeled one i.e. the vertices are identified by their indices 0,1,2,3.
Let's dig into the data structures at play here.
struct node{
int vertex;
struct node* next;
};
struct Graph{
int numVertices;
struct node** adjLists;
};
Don't let the struct node** adjLists overwhelm you.
All we are saying is we want to store a pointer to struct node*. This is because we don't know how many vertices the graph will have and so we cannot create an array of Linked Lists at compile time.
Adjacency List C++
It is the same structure but by using the in-built list STL data structures of C++, we make the structure a bit cleaner. We are also able to abstract the details of the implementation.
class Graph{
int numVertices;
list<int> *adjLists;
public:
Graph(int V);
void addEdge(int src, int dest);
};
Adjacency List Java
We use Java Collections to store the Array of Linked Lists.
class Graph{
private int numVertices;
private LinkedList<integer> adjLists[];
}
The type of LinkedList is determined by what data you want to store in it. For a labeled graph, you could store a dictionary instead of an Integer
Adjacency List Python
There is a reason Python gets so much love. A simple dictionary of vertices and its edges is a sufficient representation of a graph. You can make the vertex itself as complex as you want.
graph = {'A': set(['B', 'C']),
'B': set(['A', 'D', 'E']),
'C': set(['A', 'F']),
'D': set(['B']),
'E': set(['B', 'F']),
'F': set(['C', 'E'])}
Adjacency List Code in Python, Java, and C/C++
# Adjascency List representation in Python
class AdjNode:
def __init__(self, value):
self.vertex = value
self.next = None
class Graph:
def __init__(self, num):
self.V = num
self.graph = [None] * self.V
# Add edges
def add_edge(self, s, d):
node = AdjNode(d)
node.next = self.graph[s]
self.graph[s] = node
node = AdjNode(s)
node.next = self.graph[d]
self.graph[d] = node
# Print the graph
def print_agraph(self):
for i in range(self.V):
print("Vertex " + str(i) + ":", end="")
temp = self.graph[i]
while temp:
print(" -> {}".format(temp.vertex), end="")
temp = temp.next
print(" \n")
if __name__ == "__main__":
V = 5
# Create graph and edges
graph = Graph(V)
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(0, 3)
graph.add_edge(1, 2)
graph.print_agraph()
// Adjascency List representation in Java
import java.util.*;
class Graph {
// Add edge
static void addEdge(ArrayList<ArrayList<Integer>> am, int s, int d) {
am.get(s).add(d);
am.get(d).add(s);
}
public static void main(String[] args) {
// Create the graph
int V = 5;
ArrayList<ArrayList<Integer>> am = new ArrayList<ArrayList<Integer>>(V);
for (int i = 0; i < V; i++)
am.add(new ArrayList<Integer>());
// Add edges
addEdge(am, 0, 1);
addEdge(am, 0, 2);
addEdge(am, 0, 3);
addEdge(am, 1, 2);
printGraph(am);
}
// Print the graph
static void printGraph(ArrayList<ArrayList<Integer>> am) {
for (int i = 0; i < am.size(); i++) {
System.out.println("\nVertex " + i + ":");
for (int j = 0; j < am.get(i).size(); j++) {
System.out.print(" -> " + am.get(i).get(j));
}
System.out.println();
}
}
}
// Adjascency List representation in C
#include <stdio.h>
#include <stdlib.h>
struct node {
int vertex;
struct node* next;
};
struct node* createNode(int);
struct Graph {
int numVertices;
struct node** adjLists;
};
// Create a node
struct node* createNode(int v) {
struct node* newNode = malloc(sizeof(struct node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// Create a graph
struct Graph* createAGraph(int vertices) {
struct Graph* graph = malloc(sizeof(struct Graph));
graph->numVertices = vertices;
graph->adjLists = malloc(vertices * sizeof(struct node*));
int i;
for (i = 0; i < vertices; i++)
graph->adjLists[i] = NULL;
return graph;
}
// Add edge
void addEdge(struct Graph* graph, int s, int d) {
// Add edge from s to d
struct node* newNode = createNode(d);
newNode->next = graph->adjLists[s];
graph->adjLists[s] = newNode;
// Add edge from d to s
newNode = createNode(s);
newNode->next = graph->adjLists[d];
graph->adjLists[d] = newNode;
}
// Print the graph
void printGraph(struct Graph* graph) {
int v;
for (v = 0; v < graph->numVertices; v++) {
struct node* temp = graph->adjLists[v];
printf("\n Vertex %d\n: ", v);
while (temp) {
printf("%d -> ", temp->vertex);
temp = temp->next;
}
printf("\n");
}
}
int main() {
struct Graph* graph = createAGraph(4);
addEdge(graph, 0, 1);
addEdge(graph, 0, 2);
addEdge(graph, 0, 3);
addEdge(graph, 1, 2);
printGraph(graph);
return 0;
}
// Adjascency List representation in C++
#include <bits/stdc++.h>
using namespace std;
// Add edge
void addEdge(vector<int> adj[], int s, int d) {
adj[s].push_back(d);
adj[d].push_back(s);
}
// Print the graph
void printGraph(vector<int> adj[], int V) {
for (int d = 0; d < V; ++d) {
cout << "\n Vertex "
<< d << ":";
for (auto x : adj[d])
cout << "-> " << x;
printf("\n");
}
}
int main() {
int V = 5;
// Create a graph
vector<int> adj[V];
// Add edges
addEdge(adj, 0, 1);
addEdge(adj, 0, 2);
addEdge(adj, 0, 3);
addEdge(adj, 1, 2);
printGraph(adj, V);
}
Applications of Adjacency List
- It is faster to use adjacency lists for graphs having less number of edges.
