A backtracking algorithm is a problem-solving algorithm that uses a brute force approach for finding the desired output.
The Brute force approach tries out all the possible solutions and chooses the desired/best solutions.
The term backtracking suggests that if the current solution is not suitable, then backtrack and try other solutions. Thus, recursion is used in this approach.
This approach is used to solve problems that have multiple solutions. If you want an optimal solution, you must go for dynamic programming.
State Space Tree
A space state tree is a tree representing all the possible states (solution or nonsolution) of the problem from the root as an initial state to the leaf as a terminal state.
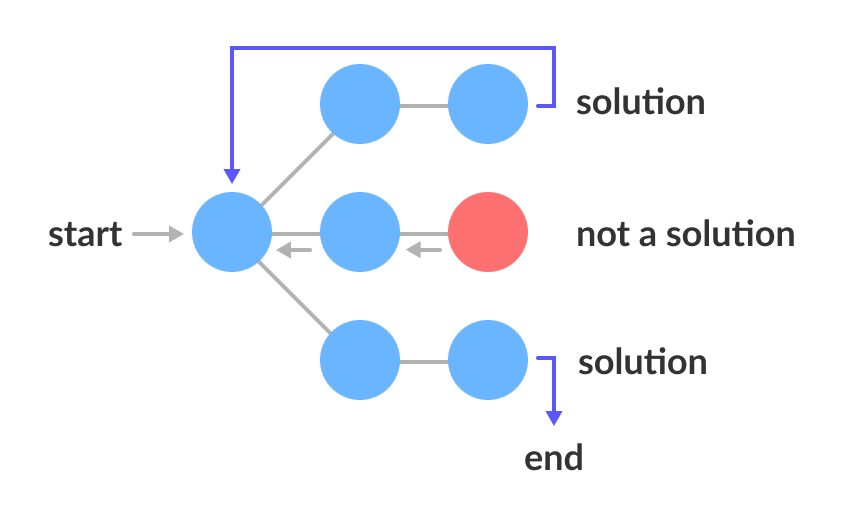
Backtracking Algorithm
Backtrack(x)
if x is not a solution
return false
if x is a new solution
add to list of solutions
backtrack(expand x)
Example Backtracking Approach
Problem: You want to find all the possible ways of arranging 2 boys and 1 girl on 3 benches. Constraint: Girl should not be on the middle bench.
Solution: There are a total of 3! = 6 possibilities. We will try all the possibilities and get the possible solutions. We recursively try all the possibilities.
All the possibilities are:

The following state space tree shows the possible solutions.

Backtracking Algorithm Applications
- To find all Hamiltonian Paths present in a graph.
- To solve the N Queen problem.
- Maze solving problem.
- The Knight's tour problem.
